Shannon-like Interpolation with Spectral Priors and Weighted Hilbert Spaces: Beyond the Nyquist Rate

In this work, we draw connections between the classical Shannon interpolation of bandlimited deterministic signals and the literature on estimating continuous-time random processes from their samples (known in various communities under different names, such as Wiener-Kolmogorov filtering, Gaussian process regression, and kriging). This leads to the realization that Shannon interpolation can be interpreted as implicitly expecting that the unknown signal has uniform spectral density within its bandwidth. However, in many practical applications, we often expect more energy at some frequencies than at others. This leads us to propose novel Shannon-like interpolators that are optimal with respect to appropriately-constructed weighted Hilbert spaces, where weighting enables us to accommodate prior information about nonuniform spectral density. Although our new interpolants are derived for data obtained with any sampling rate, we observe that they are particularly useful for interpolating sub-Nyquist data. In addition to theory, we also discuss aspects of practical implementation and show illustrative examples to demonstrate the potential benefits of the approach.

An Efficient Algorithm for Spatial-Spectral Partial Volume Compartment Mapping with Applications to Multicomponent Diffusion and Relaxation MRI

It has been previously shown that high-quality partial volume tissue compartment maps can be obtained by combining multiparametric contrast-encoded MRI data acquisition methods with spatially-regularized spectroscopic image estimation techniques. However, the advantages of this combined approach generally come at the expense of substantial computational complexity. In this work, we propose a new algorithm to solve this kind of estimation problem more efficiently. Our algorithm is based on the linearized alternating directions method of multipliers (LADMM), and relies on the introduction of novel quadratic penalty terms to substantially simplify the subproblems that must be solved at each iteration. We evaluate this algorithm on a variety of different estimation problems (diffusion-relaxation, relaxation-relaxation, relaxometry, and magnetic resonance fingerprinting), where we consistently observe substantial (roughly 5$\times$-80$\times$) speed improvements. We expect that this new faster algorithm will lower practical barriers to using spatial regularization and multiparametric contrast-encoded MRI data acquisition methods for partial volume compartment mapping.

On Optimality in ROVir

We recently published an approach named ROVir (Region-Optimized Virtual coils) that uses the beamforming capabilities of a multichannel magnetic resonance imaging (MRI) receiver array to achieve coil compression (reducing an original set of receiver channels into a much smaller number of virtual channels for the purposes of dimensionality reduction), while simultaneously preserving the MRI signal from desired spatial regions and suppressing the MRI signal arising from unwanted spatial regions. The original ROVir procedure is computationally-simple to implement (involving just a single small generalized eigendecomposition), and its signal-suppression capabilities have proven useful in an increasingly wide range of MRI applications. Our original paper made claims about the theoretical optimality of this generalized eigendecomposition procedure, but did not present the details. The purpose of this write-up is to elaborate on these mathematical details, and to introduce a new greedy iterative ROVir algorithm that enjoys certain advantages over the original ROVir calculation approach. This discussion is largely academic, with implications that we suspect will be minor for practical applications -- we have only observed small improvements to ROVir performance in the cases we have tried, and it would have been safe in these cases to still use the simpler original calculation procedure with negligible practical impact on the final imaging results.

Extended Version of "New Theory and Faster Computations for Subspace-Based Sensitivity Map Estimation in Multichannel MRI''

This is an unabridged version of a journal manuscript that has been submitted for publication [1]. (Due to length restrictions, we were forced to remove substantial amounts of content from the version that was submitted to the journal, including more detailed theoretical explanations, additional figures, and a more comprehensive bibliography. This content remains intact in this version of the document). Sensitivity map estimation is important in many multichannel MRI applications. Subspace-based sensitivity map estimation methods like ESPIRiT are popular and perform well, though can be computationally expensive and their theoretical principles can be nontrivial to understand. In the first part of this work, we present a novel theoretical derivation of subspace-based sensitivity map estimation based on a linear-predictability/structured low-rank modeling perspective. This results in an estimation approach that is equivalent to ESPIRiT, but with distinct theory that may be more intuitive for some readers. In the second part of this work, we propose and evaluate a set of computational acceleration approaches (collectively known as PISCO) that can enable substantial improvements in computation time (up to ~100x in the examples we show) and memory for subspace-based sensitivity map estimation.

On Ambiguity in Linear Inverse Problems: Entrywise Bounds on Nearly Data-Consistent Solutions and Entrywise Condition Numbers

Ill-posed linear inverse problems appear frequently in various signal processing applications. It can be very useful to have theoretical characterizations that quantify the level of ill-posedness for a given inverse problem and the degree of ambiguity that may exist about its solution. Traditional measures of ill-posedness, such as the condition number of a matrix, provide characterizations that are global in nature. While such characterizations can be powerful, they can also fail to provide full insight into situations where certain entries of the solution vector are more or less ambiguous than others. In this work, we derive novel theoretical lower- and upper-bounds that apply to individual entries of the solution vector, and are valid for all potential solution vectors that are nearly data-consistent. These bounds are agnostic to the noise statistics and the specific method used to solve the inverse problem, and are also shown to be tight. In addition, our results also lead us to introduce an entrywise version of the traditional condition number, which provides a substantially more nuanced characterization of scenarios where certain elements of the solution vector are less sensitive to perturbations than others. Our results are illustrated in an application to magnetic resonance imaging reconstruction, and we include discussions of practical computation methods for large-scale inverse problems, connections between our new theory and the traditional Cram\'{e}r-Rao bound under statistical modeling assumptions, and potential extensions to cases involving constraints beyond just data-consistency.

Robust Autocalibrated Structured Low-Rank EPI Ghost Correction

Purpose: We propose and evaluate a new structured low-rank method for EPI ghost correction called Robust Autocalibrated LORAKS (RAC-LORAKS). The method can be used to suppress EPI ghosts arising from the differences between different readout gradient polarities and/or the differences between different shots. It does not require conventional EPI navigator signals, and is robust to imperfect autocalibration data. Methods: Autocalibrated LORAKS is a previous structured low-rank method for EPI ghost correction that uses GRAPPA-type autocalibration data to enable high-quality ghost correction. This method works well when the autocalibration data is pristine, but performance degrades substantially when the autocalibration information is imperfect. RAC-LORAKS generalizes Autocalibrated LORAKS in two ways. First, it does not completely trust the information from autocalibration data, and instead considers the autocalibration and EPI data simultaneously when estimating low-rank matrix structure. And second, it uses complementary information from the autocalibration data to improve EPI reconstruction in a multi-contrast joint reconstruction framework. RAC-LORAKS is evaluated using simulations and in vivo data, and compared to state-of-the-art methods. Results: RAC-LORAKS is demonstrated to have good ghost elimination performance compared to state-of-the-art methods in several complicated acquisition scenarios (including gradient-echo brain imaging, diffusion-encoded brain imaging, and cardiac imaging). Conclusion: RAC-LORAKS provides effective suppression of EPI ghosts and is robust to imperfect autocalibration data.

LORAKI: Autocalibrated Recurrent Neural Networks for Autoregressive MRI Reconstruction in k-Space

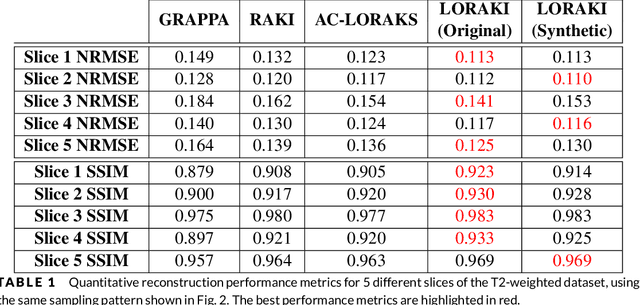
We propose and evaluate a new MRI reconstruction method named LORAKI that trains an autocalibrated scan-specific recurrent neural network (RNN) to recover missing k-space data. Methods like GRAPPA, SPIRiT, and AC-LORAKS assume that k-space data has shift-invariant autoregressive structure, and that the scan-specific autoregression relationships needed to recover missing samples can be learned from fully-sampled autocalibration (ACS) data. Recently, the structure of the linear GRAPPA method has been translated into a nonlinear deep learning method named RAKI. RAKI uses ACS data to train an artificial neural network to interpolate missing k-space samples, and often outperforms GRAPPA. In this work, we apply a similar principle to translate the linear AC-LORAKS method (simultaneously incorporating support, phase, and parallel imaging constraints) into a nonlinear deep learning method named LORAKI. Since AC-LORAKS is iterative and convolutional, LORAKI takes the form of a convolutional RNN. This new architecture admits a wide range of sampling patterns, and even calibrationless patterns are possible if synthetic ACS data is generated. The performance of LORAKI was evaluated with retrospectively undersampled brain datasets, with comparisons against other related reconstruction methods. Results suggest that LORAKI can provide improved reconstruction compared to other scan-specific autocalibrated reconstruction methods like GRAPPA, RAKI, and AC-LORAKS. LORAKI offers a new deep-learning approach to MRI reconstruction based on RNNs in k-space, and enables improved image quality and enhanced sampling flexibility.

Navigator-free EPI Ghost Correction with Structured Low-Rank Matrix Models: New Theory and Methods

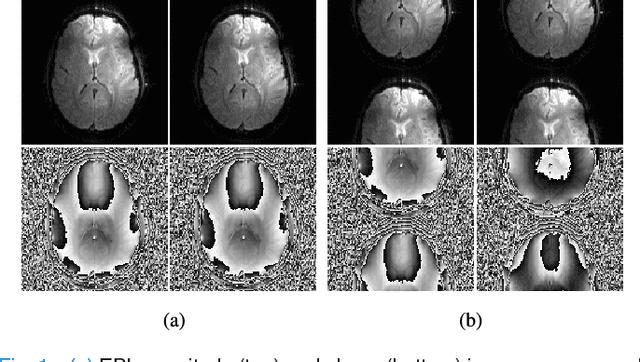
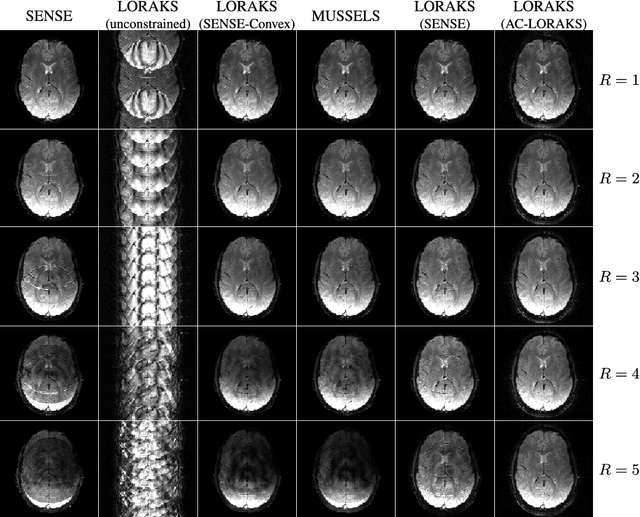
Structured low-rank matrix models have previously been introduced to enable calibrationless MR image reconstruction from sub-Nyquist data, and such ideas have recently been extended to enable navigator-free echo-planar imaging (EPI) ghost correction. This paper presents novel theoretical analysis which shows that, because of uniform subsampling, the structured low-rank matrix optimization problems for EPI data will always have either undesirable or non-unique solutions in the absence of additional constraints. This theory leads us to recommend and investigate problem formulations for navigator-free EPI that incorporate side information from either image-domain or k-space domain parallel imaging methods. The importance of using nonconvex low-rank matrix regularization is also identified. We demonstrate using phantom and \emph{in vivo} data that the proposed methods are able to eliminate ghost artifacts for several navigator-free EPI acquisition schemes, obtaining better performance in comparison to state-of-the-art methods across a range of different scenarios. Results are shown for both single-channel acquisition and highly accelerated multi-channel acquisition.