Navigator-free EPI Ghost Correction with Structured Low-Rank Matrix Models: New Theory and Methods
Paper and Code
Mar 06, 2018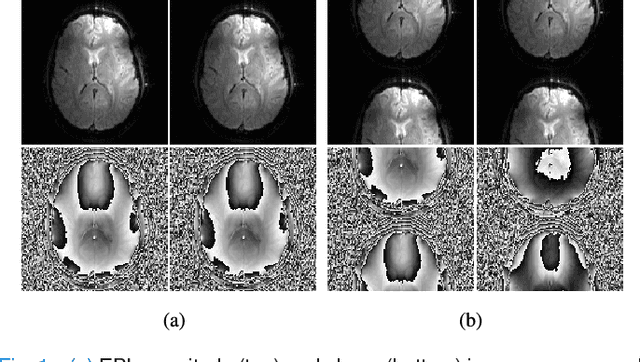


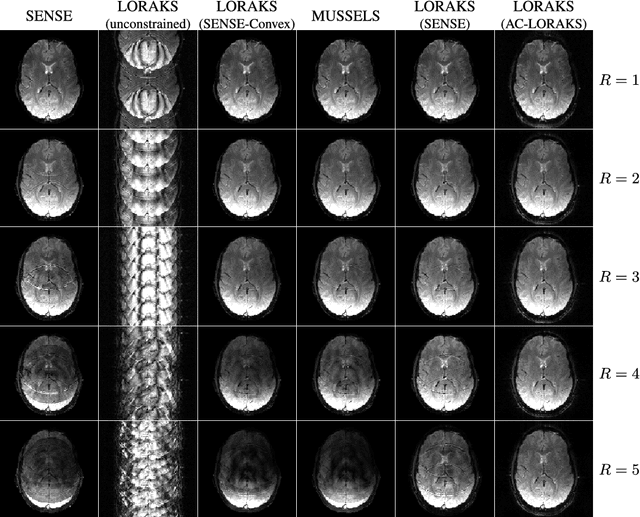
Structured low-rank matrix models have previously been introduced to enable calibrationless MR image reconstruction from sub-Nyquist data, and such ideas have recently been extended to enable navigator-free echo-planar imaging (EPI) ghost correction. This paper presents novel theoretical analysis which shows that, because of uniform subsampling, the structured low-rank matrix optimization problems for EPI data will always have either undesirable or non-unique solutions in the absence of additional constraints. This theory leads us to recommend and investigate problem formulations for navigator-free EPI that incorporate side information from either image-domain or k-space domain parallel imaging methods. The importance of using nonconvex low-rank matrix regularization is also identified. We demonstrate using phantom and \emph{in vivo} data that the proposed methods are able to eliminate ghost artifacts for several navigator-free EPI acquisition schemes, obtaining better performance in comparison to state-of-the-art methods across a range of different scenarios. Results are shown for both single-channel acquisition and highly accelerated multi-channel acquisition.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge