A$^2$ATS: Retrieval-Based KV Cache Reduction via Windowed Rotary Position Embedding and Query-Aware Vector Quantization

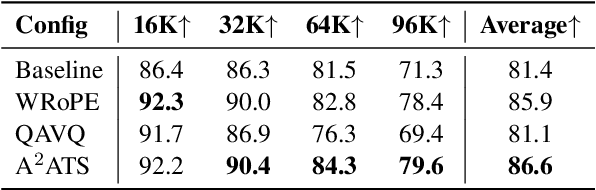
Long context large language models (LLMs) pose significant challenges for efficient serving due to the large memory footprint and high access overhead of KV cache. Retrieval-based KV cache reduction methods can mitigate these challenges, typically by offloading the complete KV cache to CPU and retrieving necessary tokens on demand during inference. However, these methods still suffer from unsatisfactory accuracy degradation and extra retrieval overhead. To address these limitations, this paper proposes A$^2$ATS, a novel retrieval-based KV cache reduction method. A$^2$ATS aims to obtain an accurate approximation of attention scores by applying the vector quantization technique to key states, thereby enabling efficient and precise retrieval of the top-K tokens. First, we propose Windowed Rotary Position Embedding, which decouples the positional dependency from query and key states after position embedding. Then, we propose query-aware vector quantization that optimizes the objective of attention score approximation directly. Finally, we design the heterogeneous inference architecture for KV cache offloading, enabling long context serving with larger batch sizes. Experimental results demonstrate that A$^2$ATS can achieve a lower performance degradation with similar or lower overhead compared to existing methods, thereby increasing long context serving throughput by up to $2.7 \times$.

CHESS: Optimizing LLM Inference via Channel-Wise Thresholding and Selective Sparsification

Deploying large language models (LLMs) on edge devices presents significant challenges due to the substantial computational overhead and memory requirements. Activation sparsification can mitigate these challenges by reducing the number of activated neurons during inference. Existing methods typically employ thresholding-based sparsification based on the statistics of activation tensors. However, these methods do not explicitly model the impact of activation sparsification on performance, leading to suboptimal performance degradation. To address this issue, this paper reformulates the activation sparsification problem by introducing a new objective that optimizes the sparsification decisions. Building on this reformulation, we propose CHESS, a general activation sparsification approach via CHannel-wise thrEsholding and Selective Sparsification. First, channel-wise thresholding assigns a unique threshold to each activation channel in the feed-forward network (FFN) layers. Then, selective sparsification involves applying thresholding-based activation sparsification to specific layers within the attention modules. Finally, we detail the implementation of sparse kernels to accelerate LLM inference. Experimental results demonstrate that the proposed CHESS achieves lower performance degradation over 8 downstream tasks while activating fewer parameters compared to existing methods, thus speeding up the LLM inference by up to 1.27x.

Adaptive Bayesian Multivariate Spline Knot Inference with Prior Specifications on Model Complexity

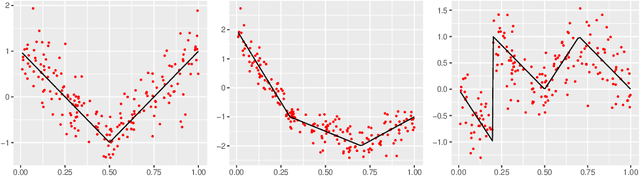
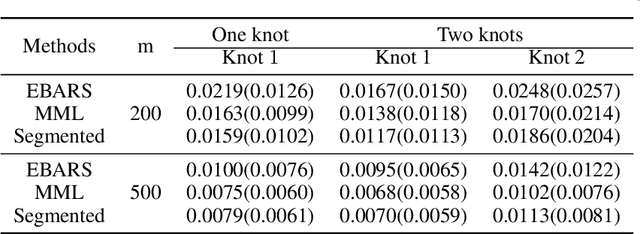
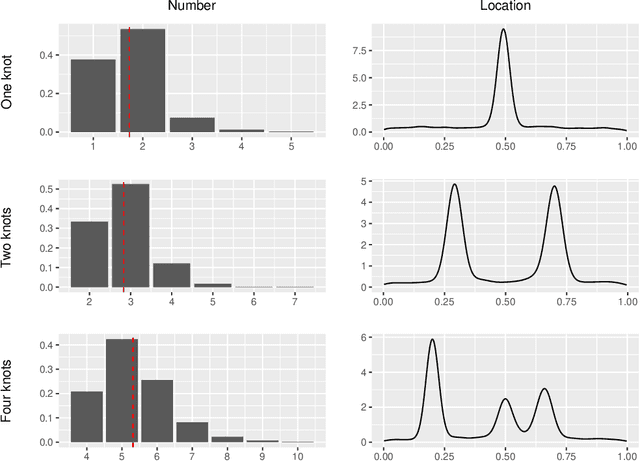
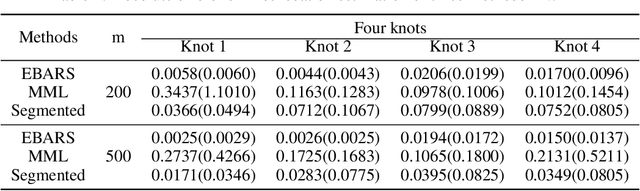
In multivariate spline regression, the number and locations of knots influence the performance and interpretability significantly. However, due to non-differentiability and varying dimensions, there is no desirable frequentist method to make inference on knots. In this article, we propose a fully Bayesian approach for knot inference in multivariate spline regression. The existing Bayesian method often uses BIC to calculate the posterior, but BIC is too liberal and it will heavily overestimate the knot number when the candidate model space is large. We specify a new prior on the knot number to take into account the complexity of the model space and derive an analytic formula in the normal model. In the non-normal cases, we utilize the extended Bayesian information criterion to approximate the posterior density. The samples are simulated in the space with differing dimensions via reversible jump Markov chain Monte Carlo. We apply the proposed method in knot inference and manifold denoising. Experiments demonstrate the splendid capability of the algorithm, especially in function fitting with jumping discontinuity.