Curved Representation Space of Vision Transformers

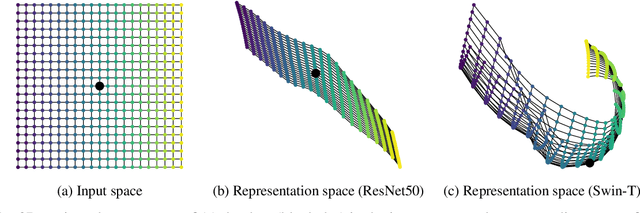
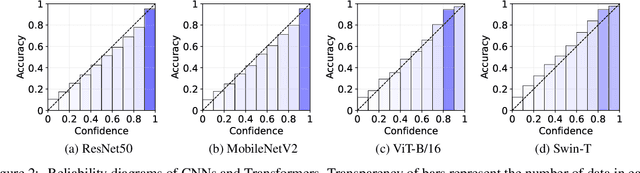
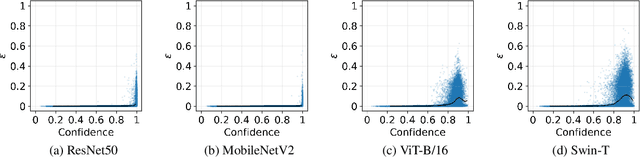
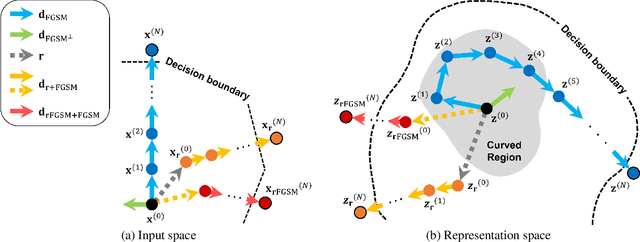
Neural networks with self-attention (a.k.a. Transformers) like ViT and Swin have emerged as a better alternative to traditional convolutional neural networks (CNNs) for computer vision tasks. However, our understanding of how the new architecture works is still limited. In this paper, we focus on the phenomenon that Transformers show higher robustness against corruptions than CNNs, while not being overconfident (in fact, we find Transformers are actually underconfident). This is contrary to the intuition that robustness increases with confidence. We resolve this contradiction by investigating how the output of the penultimate layer moves in the representation space as the input data moves within a small area. In particular, we show the following. (1) While CNNs exhibit fairly linear relationship between the input and output movements, Transformers show nonlinear relationship for some data. For those data, the output of Transformers moves in a curved trajectory as the input moves linearly. (2) When a data is located in a curved region, it is hard to move it out of the decision region since the output moves along a curved trajectory instead of a straight line to the decision boundary, resulting in high robustness of Transformers. (3) If a data is slightly modified to jump out of the curved region, the movements afterwards become linear and the output goes to the decision boundary directly. Thus, Transformers can be attacked easily after a small random jump and the perturbation in the final attacked data remains imperceptible, i.e., there does exist a decision boundary near the data. This also explains the underconfident prediction of Transformers. (4) The curved regions in the representation space start to form at an early training stage and grow throughout the training course. Some data are trapped in the regions, obstructing Transformers from reducing the training loss.

Personalized Federated Learning over non-IID Data for Indoor Localization

Localization and tracking of objects using data-driven methods is a popular topic due to the complexity in characterizing the physics of wireless channel propagation models. In these modeling approaches, data needs to be gathered to accurately train models, at the same time that user's privacy is maintained. An appealing scheme to cooperatively achieve these goals is known as Federated Learning (FL). A challenge in FL schemes is the presence of non-independent and identically distributed (non-IID) data, caused by unevenly exploration of different areas. In this paper, we consider the use of recent FL schemes to train a set of personalized models that are then optimally fused through Bayesian rules, which makes it appropriate in the context of indoor localization.