Contracting with a Learning Agent

Many real-life contractual relations differ completely from the clean, static model at the heart of principal-agent theory. Typically, they involve repeated strategic interactions of the principal and agent, taking place under uncertainty and over time. While appealing in theory, players seldom use complex dynamic strategies in practice, often preferring to circumvent complexity and approach uncertainty through learning. We initiate the study of repeated contracts with a learning agent, focusing on agents who achieve no-regret outcomes. Optimizing against a no-regret agent is a known open problem in general games; we achieve an optimal solution to this problem for a canonical contract setting, in which the agent's choice among multiple actions leads to success/failure. The solution has a surprisingly simple structure: for some $\alpha > 0$, initially offer the agent a linear contract with scalar $\alpha$, then switch to offering a linear contract with scalar $0$. This switch causes the agent to ``free-fall'' through their action space and during this time provides the principal with non-zero reward at zero cost. Despite apparent exploitation of the agent, this dynamic contract can leave \emph{both} players better off compared to the best static contract. Our results generalize beyond success/failure, to arbitrary non-linear contracts which the principal rescales dynamically. Finally, we quantify the dependence of our results on knowledge of the time horizon, and are the first to address this consideration in the study of strategizing against learning agents.

Recursive Sketches for Modular Deep Learning

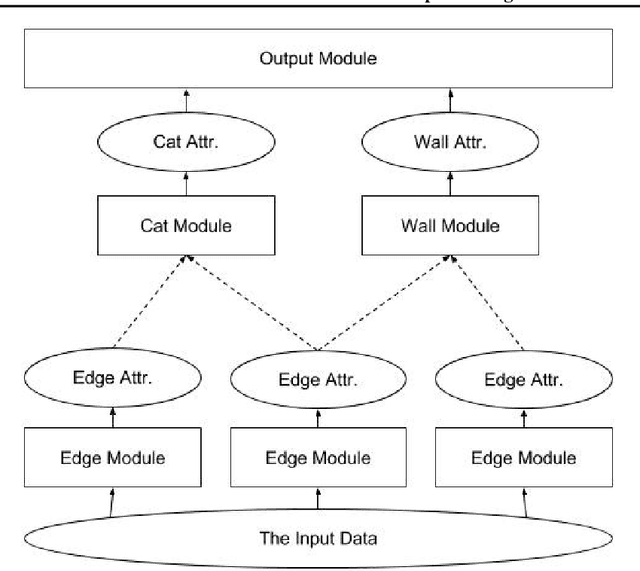
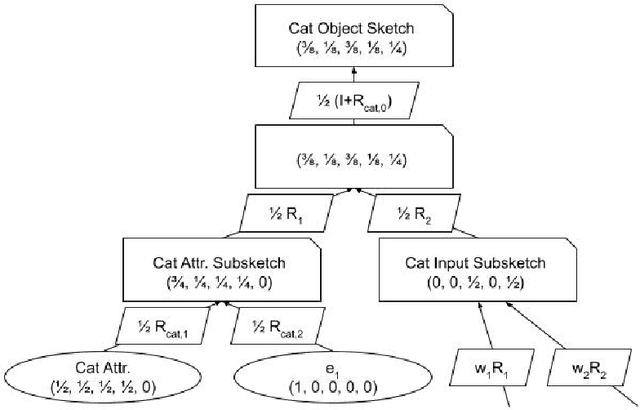
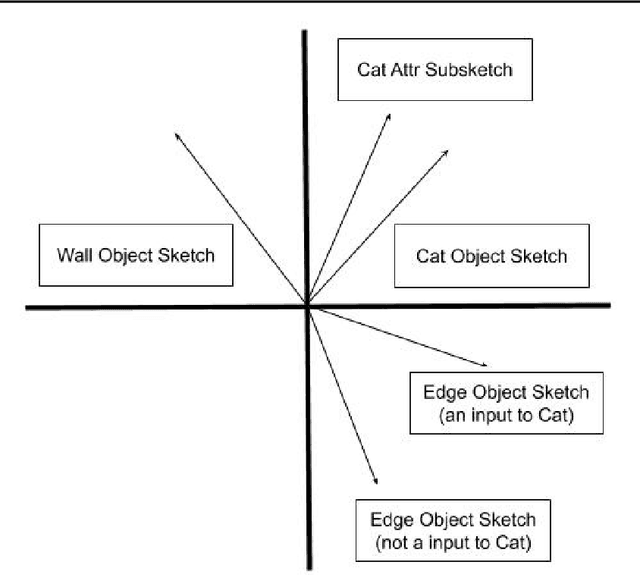
We present a mechanism to compute a sketch (succinct summary) of how a complex modular deep network processes its inputs. The sketch summarizes essential information about the inputs and outputs of the network and can be used to quickly identify key components and summary statistics of the inputs. Furthermore, the sketch is recursive and can be unrolled to identify sub-components of these components and so forth, capturing a potentially complicated DAG structure. These sketches erase gracefully; even if we erase a fraction of the sketch at random, the remainder still retains the `high-weight' information present in the original sketch. The sketches can also be organized in a repository to implicitly form a `knowledge graph'; it is possible to quickly retrieve sketches in the repository that are related to a sketch of interest; arranged in this fashion, the sketches can also be used to learn emerging concepts by looking for new clusters in sketch space. Finally, in the scenario where we want to learn a ground truth deep network, we show that augmenting input/output pairs with these sketches can theoretically make it easier to do so.

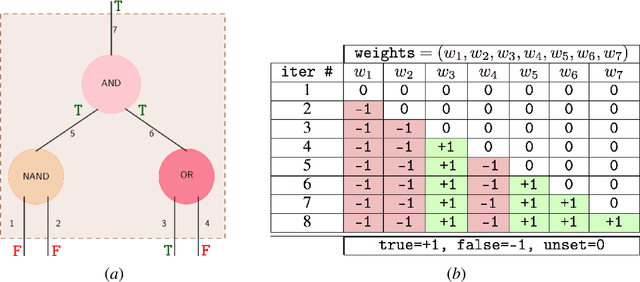
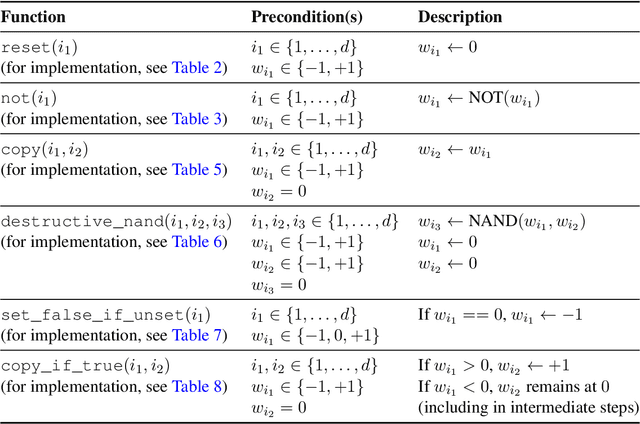
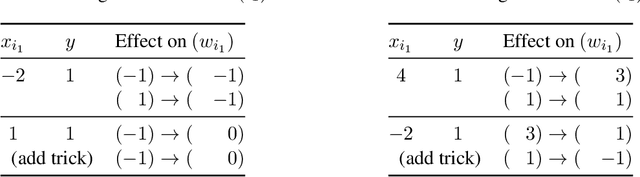
On the Computational Power of Online Gradient Descent

We prove that the evolution of weight vectors in online gradient descent can encode arbitrary polynomial-space computations, even in the special case of soft-margin support vector machines. Our results imply that, under weak complexity-theoretic assumptions, it is impossible to reason efficiently about the fine-grained behavior of online gradient descent.

An Optimal Algorithm for Online Unconstrained Submodular Maximization

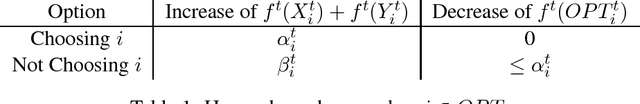
We consider a basic problem at the interface of two fundamental fields: submodular optimization and online learning. In the online unconstrained submodular maximization (online USM) problem, there is a universe $[n]=\{1,2,...,n\}$ and a sequence of $T$ nonnegative (not necessarily monotone) submodular functions arrive over time. The goal is to design a computationally efficient online algorithm, which chooses a subset of $[n]$ at each time step as a function only of the past, such that the accumulated value of the chosen subsets is as close as possible to the maximum total value of a fixed subset in hindsight. Our main result is a polynomial-time no-$1/2$-regret algorithm for this problem, meaning that for every sequence of nonnegative submodular functions, the algorithm's expected total value is at least $1/2$ times that of the best subset in hindsight, up to an error term sublinear in $T$. The factor of $1/2$ cannot be improved upon by any polynomial-time online algorithm when the submodular functions are presented as value oracles. Previous work on the offline problem implies that picking a subset uniformly at random in each time step achieves zero $1/4$-regret. A byproduct of our techniques is an explicit subroutine for the two-experts problem that has an unusually strong regret guarantee: the total value of its choices is comparable to twice the total value of either expert on rounds it did not pick that expert. This subroutine may be of independent interest.

Optimal Algorithms for Continuous Non-monotone Submodular and DR-Submodular Maximization

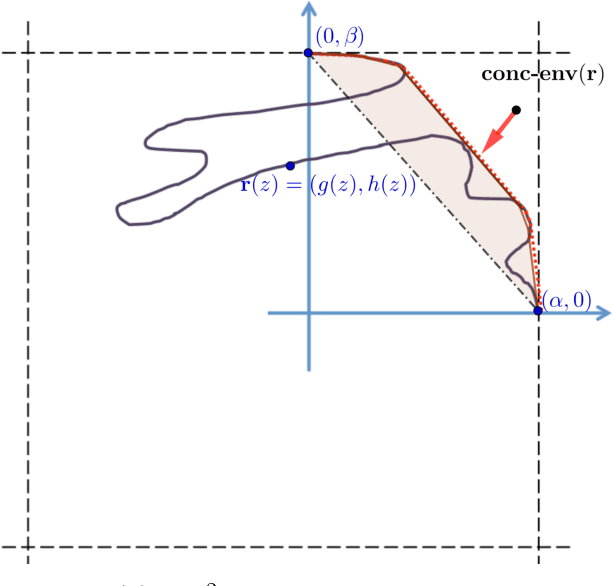
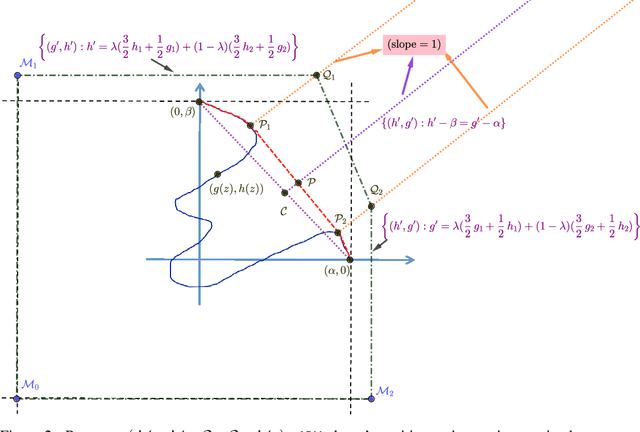
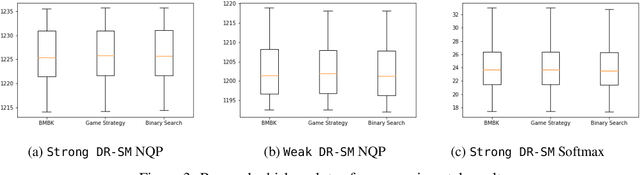
In this paper we study the fundamental problems of maximizing a continuous non-monotone submodular function over the hypercube, both with and without coordinate-wise concavity. This family of optimization problems has several applications in machine learning, economics, and communication systems. Our main result is the first $\frac{1}{2}$-approximation algorithm for continuous submodular function maximization; this approximation factor of $\frac{1}{2}$ is the best possible for algorithms that only query the objective function at polynomially many points. For the special case of DR-submodular maximization, i.e. when the submodular functions is also coordinate wise concave along all coordinates, we provide a different $\frac{1}{2}$-approximation algorithm that runs in quasilinear time. Both of these results improve upon prior work [Bian et al, 2017, Soma and Yoshida, 2017]. Our first algorithm uses novel ideas such as reducing the guaranteed approximation problem to analyzing a zero-sum game for each coordinate, and incorporates the geometry of this zero-sum game to fix the value at this coordinate. Our second algorithm exploits coordinate-wise concavity to identify a monotone equilibrium condition sufficient for getting the required approximation guarantee, and hunts for the equilibrium point using binary search. We further run experiments to verify the performance of our proposed algorithms in related machine learning applications.