An Optimal Algorithm for Online Unconstrained Submodular Maximization
Paper and Code
Jun 08, 2018
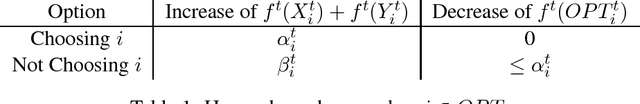
We consider a basic problem at the interface of two fundamental fields: submodular optimization and online learning. In the online unconstrained submodular maximization (online USM) problem, there is a universe $[n]=\{1,2,...,n\}$ and a sequence of $T$ nonnegative (not necessarily monotone) submodular functions arrive over time. The goal is to design a computationally efficient online algorithm, which chooses a subset of $[n]$ at each time step as a function only of the past, such that the accumulated value of the chosen subsets is as close as possible to the maximum total value of a fixed subset in hindsight. Our main result is a polynomial-time no-$1/2$-regret algorithm for this problem, meaning that for every sequence of nonnegative submodular functions, the algorithm's expected total value is at least $1/2$ times that of the best subset in hindsight, up to an error term sublinear in $T$. The factor of $1/2$ cannot be improved upon by any polynomial-time online algorithm when the submodular functions are presented as value oracles. Previous work on the offline problem implies that picking a subset uniformly at random in each time step achieves zero $1/4$-regret. A byproduct of our techniques is an explicit subroutine for the two-experts problem that has an unusually strong regret guarantee: the total value of its choices is comparable to twice the total value of either expert on rounds it did not pick that expert. This subroutine may be of independent interest.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge