Borinot: an agile torque-controlled robot for hybrid flying and contact loco-manipulation

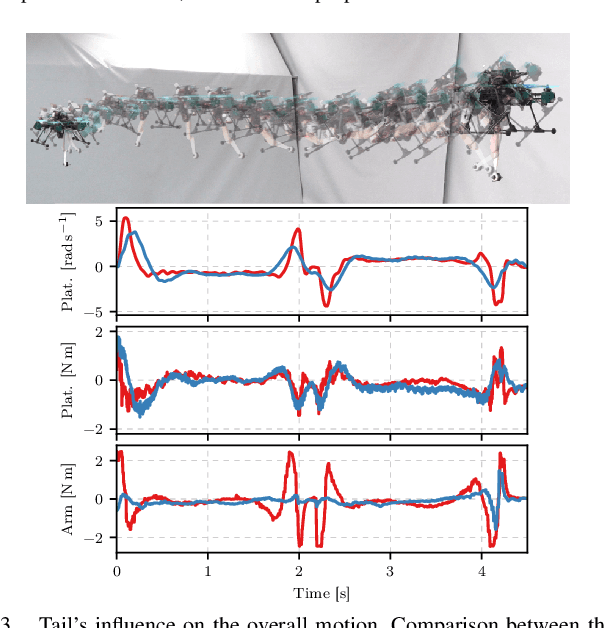
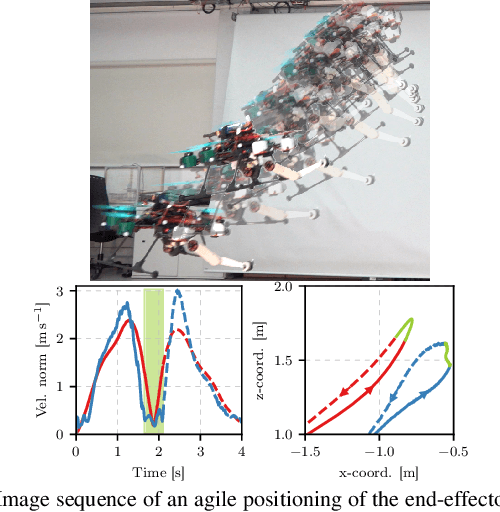
This paper introduces Borinot, an open-source flying robotic platform designed to perform hybrid agile locomotion and manipulation. This platform features a compact and powerful hexarotor that can be outfitted with torque-actuated extremities of diverse architecture, allowing for whole-body dynamic control. As a result, Borinot can perform agile tasks such as aggressive or acrobatic maneuvers with the participation of the whole-body dynamics. The extremities attached to Borinot can be utilized in various ways; during contact, they can be used as legs to create contact-based locomotion, or as arms to manipulate objects. In free flight, they can be used as tails to contribute to dynamics, mimicking the movements of many animals. This allows for any hybridization of these dynamic modes, like the jump-flight of chicken and locusts, making Borinot an ideal open-source platform for research on hybrid aerial-contact agile motion. To demonstrate the key capabilities of Borinot, we have fitted a planar 2DoF arm and implemented whole-body torque-level model-predictive-control. The result is a capable and adaptable platform that, we believe, opens up new avenues of research in the field of agile robotics.

A Direct-Indirect Hybridization Approach to Control-Limited DDP

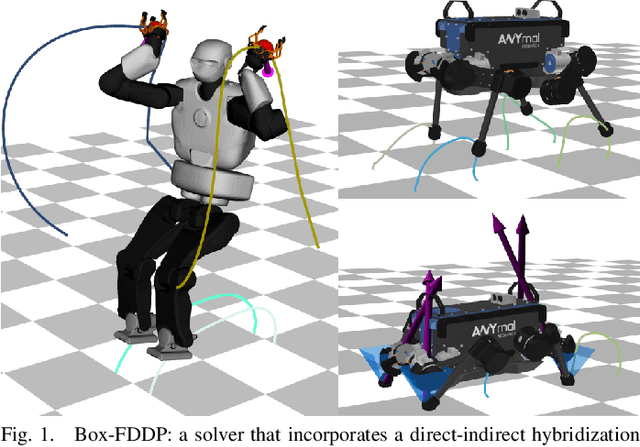
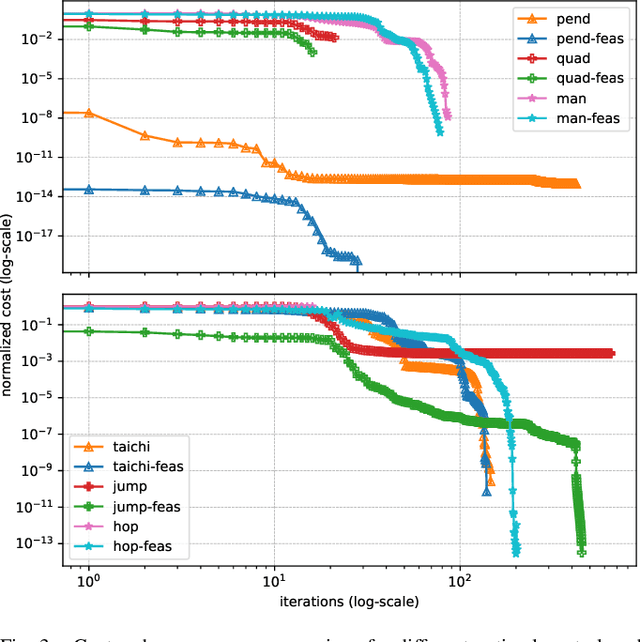
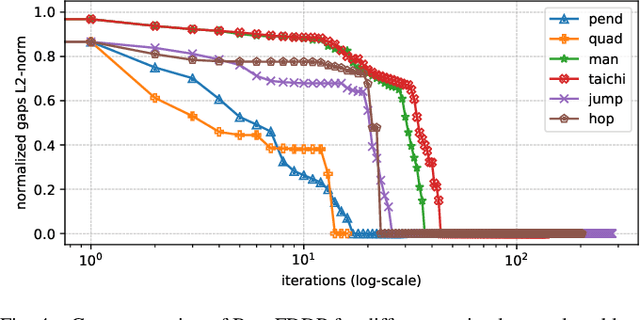
Optimal control is a widely used tool for synthesizing motions and controls for user-defined tasks under physical constraints. A common approach is to formulate it using direct multiple-shooting and then to use off-the-shelf nonlinear programming solvers that can easily handle arbitrary constraints on the controls and states. However, these methods are not fast enough for many robotics applications such as real-time humanoid motor control. Exploiting the sparse structure of optimal control problem, such as in Differential DynamicProgramming (DDP), has proven to significantly boost the computational efficiency, and recent works have been focused on handling arbitrary constraints. Despite that, DDP has been associated with poor numerical convergence, particularly when considering long time horizons. One of the main reasons is due to system instabilities and poor warm-starting (only controls). This paper presents control-limited Feasibility-driven DDP (Box-FDDP), a solver that incorporates a direct-indirect hybridization of the control-limited DDP algorithm. Concretely, the forward and backward passes handle feasibility and control limits. We showcase the impact and importance of our method on a set of challenging optimal control problems against the Box-DDP and squashing-function approach.

Multi-task closed-loop inverse kinematics stability through semidefinite programming

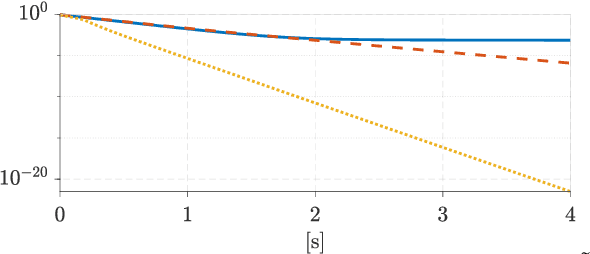
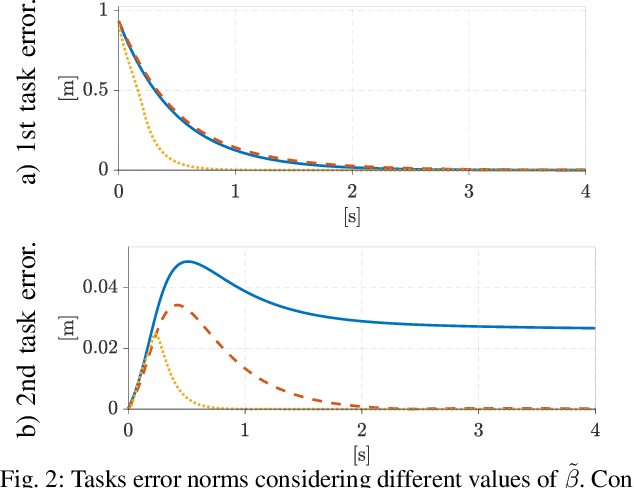
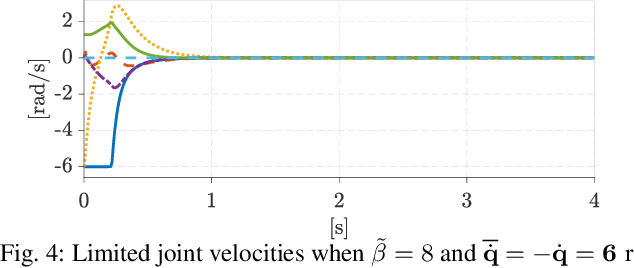
Today's complex robotic designs comprise in some cases a large number of degrees of freedom, enabling for multi-objective task resolution (e.g., humanoid robots or aerial manipulators). This paper tackles the stability problem of a hierarchical losed-loop inverse kinematics algorithm for such highly redundant robots. We present a method to guarantee system stability by performing an online tuning of the closedloop control gains. We define a semi-definite programming problem (SDP) with these gains as decision variables and a discrete-time Lyapunov stability condition as a linear matrix inequality, constraining the SDP optimization problem and guaranteeing the stability of the prioritized tasks. To the best of authors' knowledge, this work represents the first mathematical development of an SDP formulation that introduces stability conditions for a multi-objective closed-loop inverse kinematic problem for highly redundant robots. The validity of the proposed approach is demonstrated through simulation case studies, including didactic examples and a Matlab toolbox for the benefit of the community.