Linear quadratic control of nonlinear systems with Koopman operator learning and the Nyström method

In this paper, we study how the Koopman operator framework can be combined with kernel methods to effectively control nonlinear dynamical systems. While kernel methods have typically large computational requirements, we show how random subspaces (Nystr\"om approximation) can be used to achieve huge computational savings while preserving accuracy. Our main technical contribution is deriving theoretical guarantees on the effect of the Nystr\"om approximation. More precisely, we study the linear quadratic regulator problem, showing that both the approximated Riccati operator and the regulator objective, for the associated solution of the optimal control problem, converge at the rate $m^{-1/2}$, where $m$ is the random subspace size. Theoretical findings are complemented by numerical experiments corroborating our results.

Model Predictive Control for Dynamic Cloth Manipulation: Parameter Learning and Experimental Validation

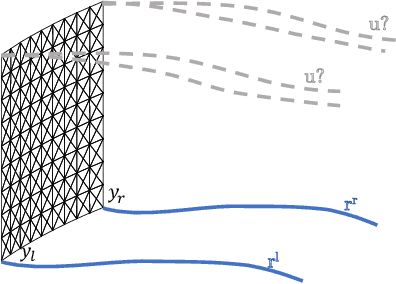
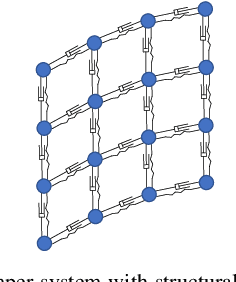
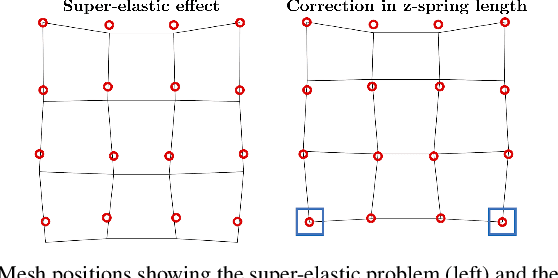
Robotic cloth manipulation is a relevant challenging problem for autonomous robotic systems. Highly deformable objects as textile items can adopt multiple configurations and shapes during their manipulation. Hence, robots should not only understand the current cloth configuration but also be able to predict the future possible behaviors of the cloth. This paper addresses the problem of indirectly controlling the configuration of certain points of a textile object, by applying actions on other parts of the object through the use of a Model Predictive Control (MPC) strategy, which also allows to foresee the behavior of indirectly controlled points. The designed controller finds the optimal control signals to attain the desired future target configuration. The explored scenario in this paper considers tracking a reference trajectory with the lower corners of a square piece of cloth by grasping its upper corners. To do so, we propose and validate a linear cloth model that allows solving the MPC-related optimization problem in real time. Reinforcement Learning (RL) techniques are used to learn the optimal parameters of the proposed cloth model and also to tune the resulting MPC. After obtaining accurate tracking results in simulation, the full control scheme was implemented and executed in a real robot, obtaining accurate tracking even in adverse conditions. While total observed errors reach the 5 cm mark, for a 30x30 cm cloth, an analysis shows the MPC contributes less than 30% to that value.

Multi-task closed-loop inverse kinematics stability through semidefinite programming

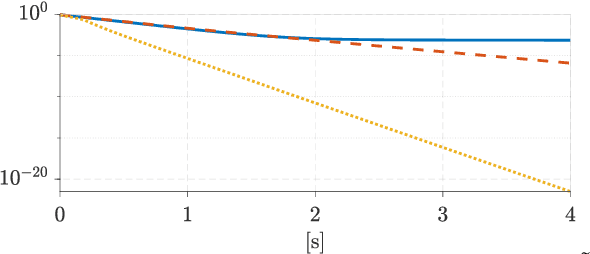
Today's complex robotic designs comprise in some cases a large number of degrees of freedom, enabling for multi-objective task resolution (e.g., humanoid robots or aerial manipulators). This paper tackles the stability problem of a hierarchical losed-loop inverse kinematics algorithm for such highly redundant robots. We present a method to guarantee system stability by performing an online tuning of the closedloop control gains. We define a semi-definite programming problem (SDP) with these gains as decision variables and a discrete-time Lyapunov stability condition as a linear matrix inequality, constraining the SDP optimization problem and guaranteeing the stability of the prioritized tasks. To the best of authors' knowledge, this work represents the first mathematical development of an SDP formulation that introduces stability conditions for a multi-objective closed-loop inverse kinematic problem for highly redundant robots. The validity of the proposed approach is demonstrated through simulation case studies, including didactic examples and a Matlab toolbox for the benefit of the community.