Multi-resolution Guided 3D GANs for Medical Image Translation

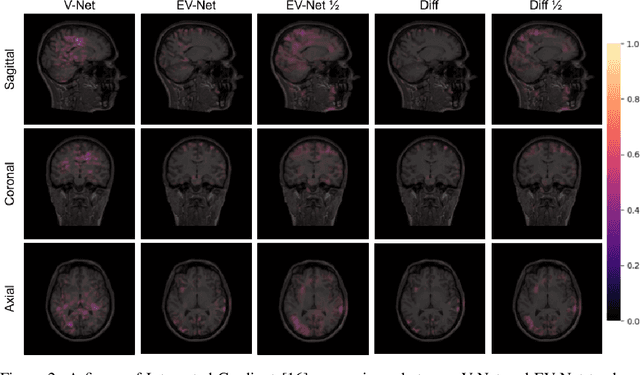
Medical image translation is the process of converting from one imaging modality to another, in order to reduce the need for multiple image acquisitions from the same patient. This can enhance the efficiency of treatment by reducing the time, equipment, and labor needed. In this paper, we introduce a multi-resolution guided Generative Adversarial Network (GAN)-based framework for 3D medical image translation. Our framework uses a 3D multi-resolution Dense-Attention UNet (3D-mDAUNet) as the generator and a 3D multi-resolution UNet as the discriminator, optimized with a unique combination of loss functions including voxel-wise GAN loss and 2.5D perception loss. Our approach yields promising results in volumetric image quality assessment (IQA) across a variety of imaging modalities, body regions, and age groups, demonstrating its robustness. Furthermore, we propose a synthetic-to-real applicability assessment as an additional evaluation to assess the effectiveness of synthetic data in downstream applications such as segmentation. This comprehensive evaluation shows that our method produces synthetic medical images not only of high-quality but also potentially useful in clinical applications. Our code is available at github.com/juhha/3D-mADUNet.

EVC-Net: Multi-scale V-Net with Conditional Random Fields for Brain Extraction

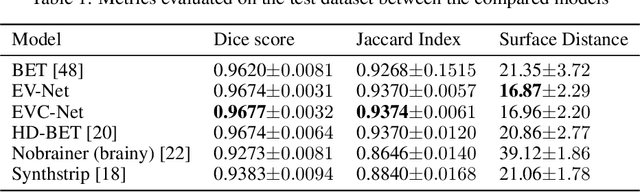
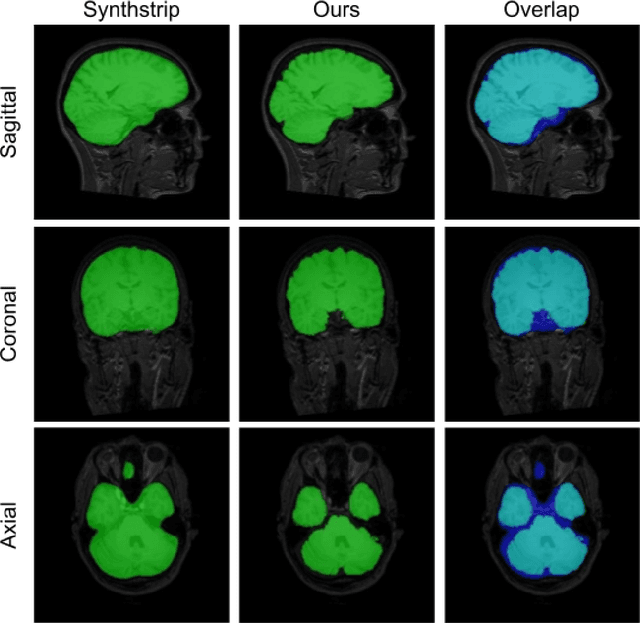
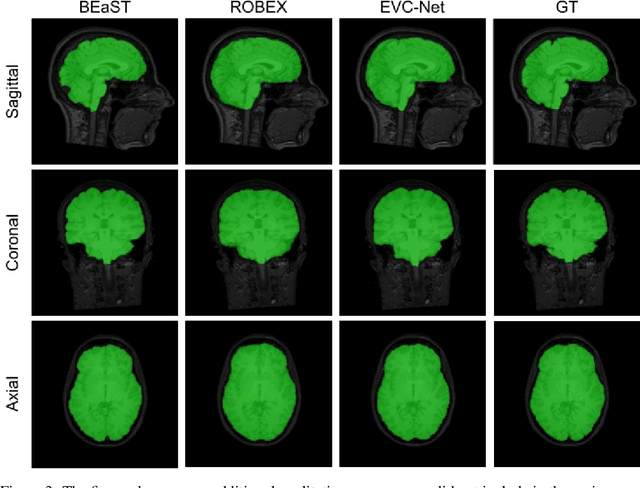
Brain extraction is one of the first steps of pre-processing 3D brain MRI data. It is a prerequisite for any forthcoming brain imaging analyses. However, it is not a simple segmentation problem due to the complex structure of the brain and human head. Although multiple solutions have been proposed in the literature, we are still far from having truly robust methods. While previous methods have used machine learning with structural/geometric priors, with the development of deep learning in computer vision tasks, there has been an increase in proposed convolutional neural network architectures for this semantic segmentation task. Yet, most models focus on improving the training data and loss functions with little change in the architecture. In this paper, we propose a novel architecture we call EVC-Net. EVC-Net adds lower scale inputs on each encoder block. This enhances the multi-scale scheme of the V-Net architecture, hence increasing the efficiency of the model. Conditional Random Fields, a popular approach for image segmentation before the deep learning era, are re-introduced here as an additional step for refining the network's output to capture fine-grained results in segmentation. We compare our model to state-of-the-art methods such as HD-BET, Synthstrip and brainy. Results show that even with limited training resources, EVC-Net achieves higher Dice Coefficient and Jaccard Index along with lower surface distance.

ThetA -- fast and robust clustering via a distance parameter

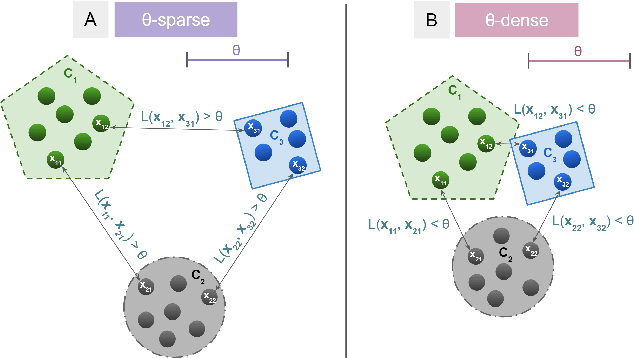
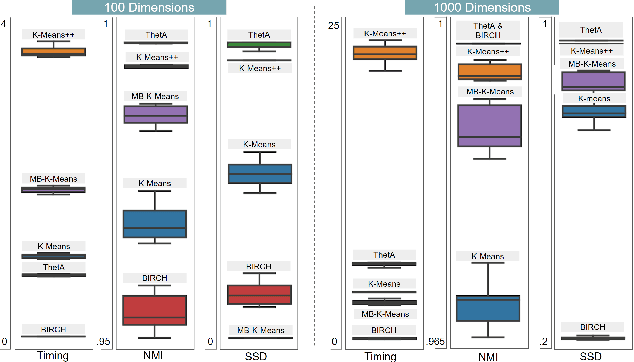
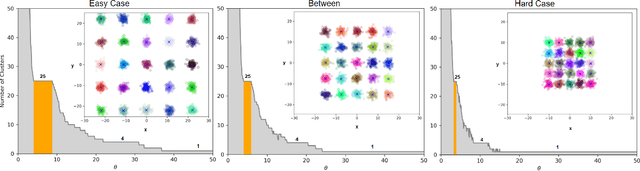
Clustering is a fundamental problem in machine learning where distance-based approaches have dominated the field for many decades. This set of problems is often tackled by partitioning the data into K clusters where the number of clusters is chosen apriori. While significant progress has been made on these lines over the years, it is well established that as the number of clusters or dimensions increase, current approaches dwell in local minima resulting in suboptimal solutions. In this work, we propose a new set of distance threshold methods called Theta-based Algorithms (ThetA). Via experimental comparisons and complexity analyses we show that our proposed approach outperforms existing approaches in: a) clustering accuracy and b) time complexity. Additionally, we show that for a large class of problems, learning the optimal threshold is straightforward in comparison to learning K. Moreover, we show how ThetA can infer the sparsity of datasets in higher dimensions.