Designing Machine Learning Surrogates using Outputs of Molecular Dynamics Simulations as Soft Labels

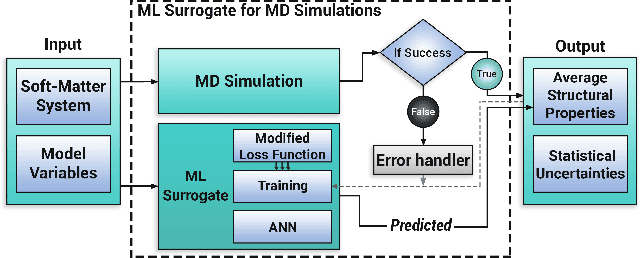
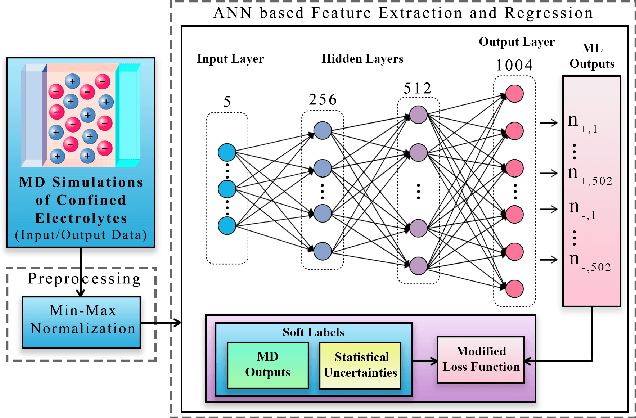
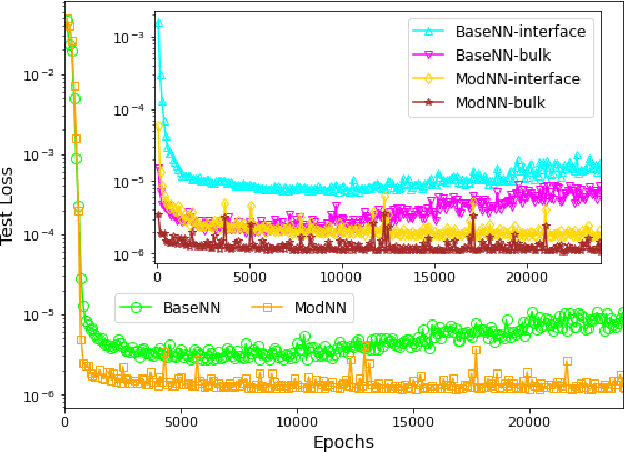
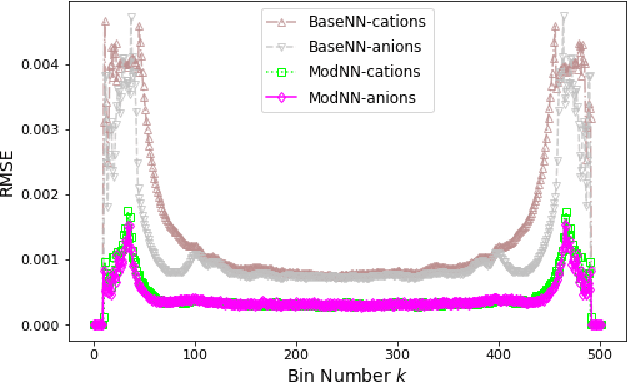
Molecular dynamics simulations are powerful tools to extract the microscopic mechanisms characterizing the properties of soft materials. We recently introduced machine learning surrogates for molecular dynamics simulations of soft materials and demonstrated that artificial neural network based regression models can successfully predict the relationships between the input material attributes and the simulation outputs. Here, we show that statistical uncertainties associated with the outputs of molecular dynamics simulations can be utilized to train artificial neural networks and design machine learning surrogates with higher accuracy and generalizability. We design soft labels for the simulation outputs by incorporating the uncertainties in the estimated average output quantities, and introduce a modified loss function that leverages these soft labels during training to significantly reduce the surrogate prediction error for input systems in the unseen test data. The approach is illustrated with the design of a surrogate for molecular dynamics simulations of confined electrolytes to predict the complex relationship between the input electrolyte attributes and the output ionic structure. The surrogate predictions for the ionic density profiles show excellent agreement with the ground truth results produced using molecular dynamics simulations. The high accuracy and small inference times associated with the surrogate predictions provide quick access to quantities derived using the number density profiles and facilitate rapid sensitivity analysis.

ThetA -- fast and robust clustering via a distance parameter

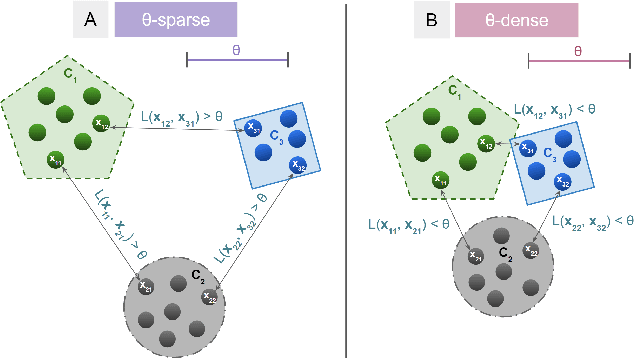
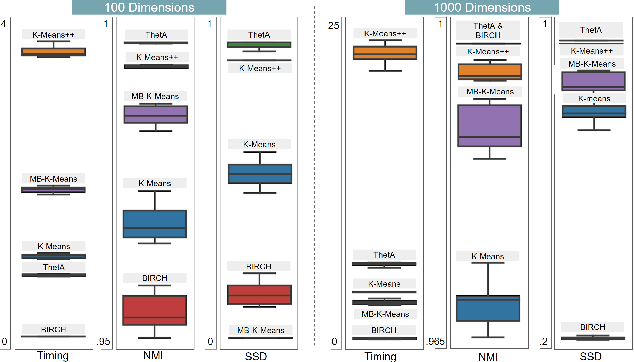
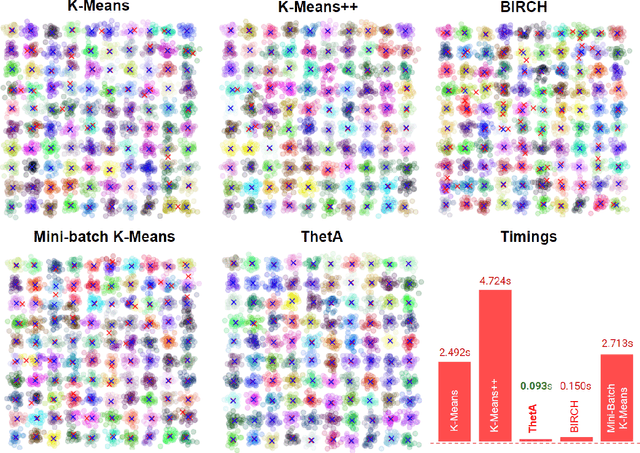
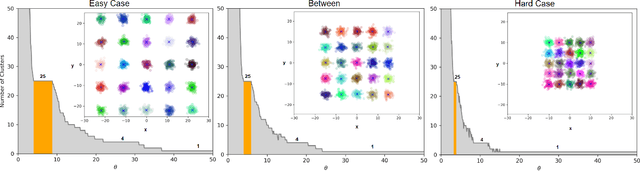
Clustering is a fundamental problem in machine learning where distance-based approaches have dominated the field for many decades. This set of problems is often tackled by partitioning the data into K clusters where the number of clusters is chosen apriori. While significant progress has been made on these lines over the years, it is well established that as the number of clusters or dimensions increase, current approaches dwell in local minima resulting in suboptimal solutions. In this work, we propose a new set of distance threshold methods called Theta-based Algorithms (ThetA). Via experimental comparisons and complexity analyses we show that our proposed approach outperforms existing approaches in: a) clustering accuracy and b) time complexity. Additionally, we show that for a large class of problems, learning the optimal threshold is straightforward in comparison to learning K. Moreover, we show how ThetA can infer the sparsity of datasets in higher dimensions.