MICCAI-CDMRI 2023 QuantConn Challenge Findings on Achieving Robust Quantitative Connectivity through Harmonized Preprocessing of Diffusion MRI

White matter alterations are increasingly implicated in neurological diseases and their progression. International-scale studies use diffusion-weighted magnetic resonance imaging (DW-MRI) to qualitatively identify changes in white matter microstructure and connectivity. Yet, quantitative analysis of DW-MRI data is hindered by inconsistencies stemming from varying acquisition protocols. There is a pressing need to harmonize the preprocessing of DW-MRI datasets to ensure the derivation of robust quantitative diffusion metrics across acquisitions. In the MICCAI-CDMRI 2023 QuantConn challenge, participants were provided raw data from the same individuals collected on the same scanner but with two different acquisitions and tasked with preprocessing the DW-MRI to minimize acquisition differences while retaining biological variation. Submissions are evaluated on the reproducibility and comparability of cross-acquisition bundle-wise microstructure measures, bundle shape features, and connectomics. The key innovations of the QuantConn challenge are that (1) we assess bundles and tractography in the context of harmonization for the first time, (2) we assess connectomics in the context of harmonization for the first time, and (3) we have 10x additional subjects over prior harmonization challenge, MUSHAC and 100x over SuperMUDI. We find that bundle surface area, fractional anisotropy, connectome assortativity, betweenness centrality, edge count, modularity, nodal strength, and participation coefficient measures are most biased by acquisition and that machine learning voxel-wise correction, RISH mapping, and NeSH methods effectively reduce these biases. In addition, microstructure measures AD, MD, RD, bundle length, connectome density, efficiency, and path length are least biased by these acquisition differences.

ThetA -- fast and robust clustering via a distance parameter

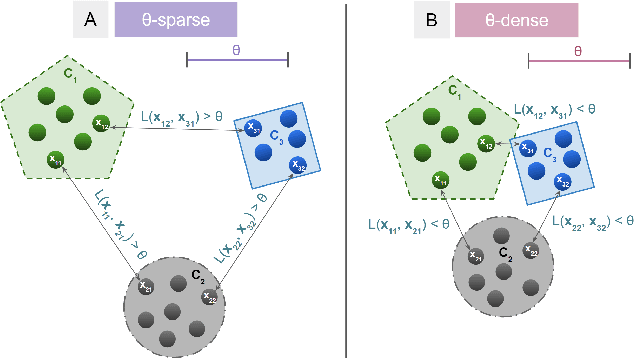
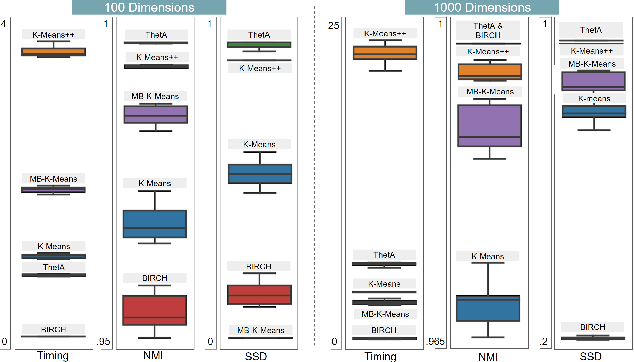
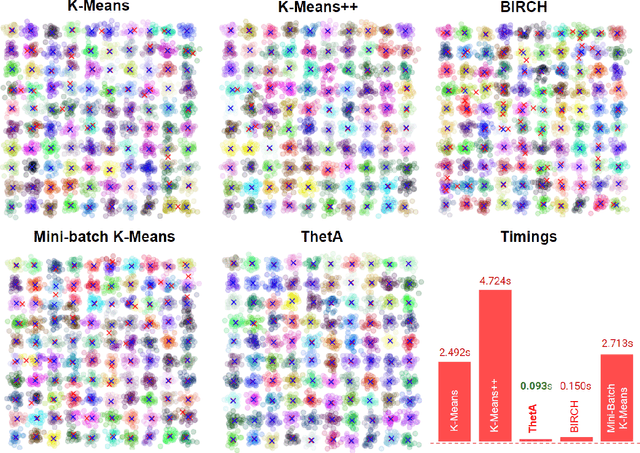
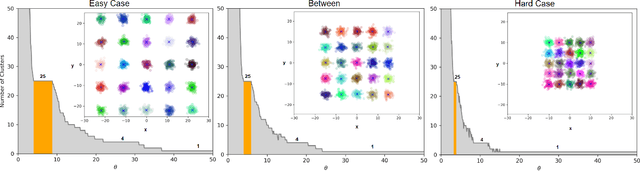
Clustering is a fundamental problem in machine learning where distance-based approaches have dominated the field for many decades. This set of problems is often tackled by partitioning the data into K clusters where the number of clusters is chosen apriori. While significant progress has been made on these lines over the years, it is well established that as the number of clusters or dimensions increase, current approaches dwell in local minima resulting in suboptimal solutions. In this work, we propose a new set of distance threshold methods called Theta-based Algorithms (ThetA). Via experimental comparisons and complexity analyses we show that our proposed approach outperforms existing approaches in: a) clustering accuracy and b) time complexity. Additionally, we show that for a large class of problems, learning the optimal threshold is straightforward in comparison to learning K. Moreover, we show how ThetA can infer the sparsity of datasets in higher dimensions.