Stable Formulations in Optimistic Bilevel Optimization

Solutions of bilevel optimization problems tend to suffer from instability under changes to problem data. In the optimistic setting, we construct a lifted, alternative formulation that exhibits desirable stability properties under mild assumptions that neither invoke convexity nor smoothness. The upper- and lower-level problems might involve integer restrictions and disjunctive constraints. In a range of results, we at most invoke pointwise and local calmness for the lower-level problem in a sense that holds broadly. The alternative formulation is computationally attractive with structural properties being brought out and an outer approximation algorithm becoming available.

Mitigating the Impact of Labeling Errors on Training via Rockafellian Relaxation

Labeling errors in datasets are common, if not systematic, in practice. They naturally arise in a variety of contexts-human labeling, noisy labeling, and weak labeling (i.e., image classification), for example. This presents a persistent and pervasive stress on machine learning practice. In particular, neural network (NN) architectures can withstand minor amounts of dataset imperfection with traditional countermeasures such as regularization, data augmentation, and batch normalization. However, major dataset imperfections often prove insurmountable. We propose and study the implementation of Rockafellian Relaxation (RR), a new loss reweighting, architecture-independent methodology, for neural network training. Experiments indicate RR can enhance standard neural network methods to achieve robust performance across classification tasks in computer vision and natural language processing (sentiment analysis). We find that RR can mitigate the effects of dataset corruption due to both (heavy) labeling error and/or adversarial perturbation, demonstrating effectiveness across a variety of data domains and machine learning tasks.

On Memorization and Privacy risks of Sharpness Aware Minimization

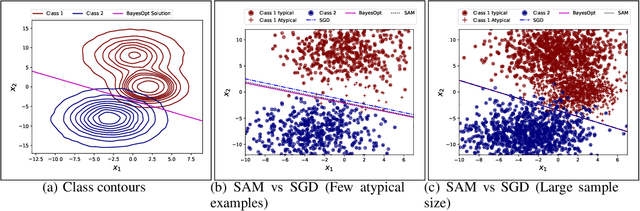
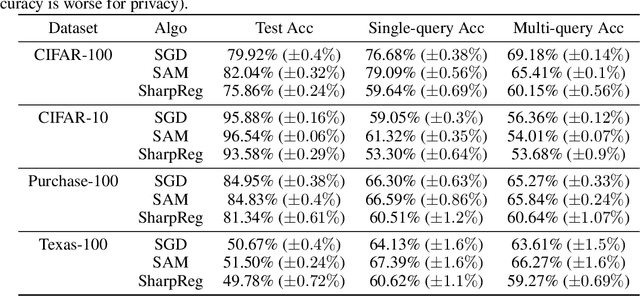
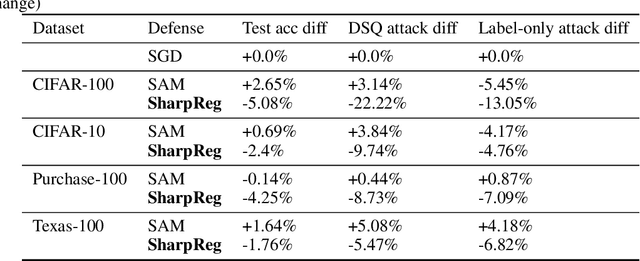
In many recent works, there is an increased focus on designing algorithms that seek flatter optima for neural network loss optimization as there is empirical evidence that it leads to better generalization performance in many datasets. In this work, we dissect these performance gains through the lens of data memorization in overparameterized models. We define a new metric that helps us identify which data points specifically do algorithms seeking flatter optima do better when compared to vanilla SGD. We find that the generalization gains achieved by Sharpness Aware Minimization (SAM) are particularly pronounced for atypical data points, which necessitate memorization. This insight helps us unearth higher privacy risks associated with SAM, which we verify through exhaustive empirical evaluations. Finally, we propose mitigation strategies to achieve a more desirable accuracy vs privacy tradeoff.

Risk-Adaptive Approaches to Learning and Decision Making: A Survey

Uncertainty is prevalent in engineering design, statistical learning, and decision making broadly. Due to inherent risk-averseness and ambiguity about assumptions, it is common to address uncertainty by formulating and solving conservative optimization models expressed using measure of risk and related concepts. We survey the rapid development of risk measures over the last quarter century. From its beginning in financial engineering, we recount their spread to nearly all areas of engineering and applied mathematics. Solidly rooted in convex analysis, risk measures furnish a general framework for handling uncertainty with significant computational and theoretical advantages. We describe the key facts, list several concrete algorithms, and provide an extensive list of references for further reading. The survey recalls connections with utility theory and distributionally robust optimization, points to emerging applications areas such as fair machine learning, and defines measures of reliability.

On Robustness in Nonconvex Optimization with Application to Defense Planning

In the context of structured nonconvex optimization, we estimate the increase in minimum value for a decision that is robust to parameter perturbations as compared to the value of a nominal problem. The estimates rely on detailed expressions for subgradients and local Lipschitz moduli of min-value functions in nonconvex robust optimization and require only the solution of the nominal problem. The theoretical results are illustrated by examples from military operations research involving mixed-integer optimization models. Across 54 cases examined, the median error in estimating the increase in minimum value is 12%. Therefore, the derived expressions for subgradients and local Lipschitz moduli may accurately inform analysts about the possibility of obtaining cost-effective, parameter-robust decisions in nonconvex optimization.

Rockafellian Relaxation in Optimization under Uncertainty: Asymptotically Exact Formulations

In practice, optimization models are often prone to unavoidable inaccuracies due to lack of data and dubious assumptions. Traditionally, this placed special emphasis on risk-based and robust formulations, and their focus on "conservative" decisions. We develop, in contrast, an "optimistic" framework based on Rockafellian relaxations in which optimization is conducted not only over the original decision space but also jointly with a choice of model perturbation. The framework enables us to address challenging problems with ambiguous probability distributions from the areas of two-stage stochastic optimization without relatively complete recourse, probability functions lacking continuity properties, expectation constraints, and outlier analysis. We are also able to circumvent the fundamental difficulty in stochastic optimization that convergence of distributions fails to guarantee convergence of expectations. The framework centers on the novel concepts of exact and asymptotically exact Rockafellians, with interpretations of "negative" regularization emerging in certain settings. We illustrate the role of Phi-divergence, examine rates of convergence under changing distributions, and explore extensions to first-order optimality conditions. The main development is free of assumptions about convexity, smoothness, and even continuity of objective functions.

Consistent Approximations in Composite Optimization

Approximations of optimization problems arise in computational procedures and sensitivity analysis. The resulting effect on solutions can be significant, with even small approximations of components of a problem translating into large errors in the solutions. We specify conditions under which approximations are well behaved in the sense of minimizers, stationary points, and level-sets and this leads to a framework of consistent approximations. The framework is developed for a broad class of composite problems, which are neither convex nor smooth. We demonstrate the framework using examples from stochastic optimization, neural-network based machine learning, distributionally robust optimization, penalty and augmented Lagrangian methods, interior-point methods, homotopy methods, smoothing methods, extended nonlinear programming, difference-of-convex programming, and multi-objective optimization. An enhanced proximal method illustrates the algorithmic possibilities. A quantitative analysis supplements the development by furnishing rates of convergence.

Gradients and Subgradients of Buffered Failure Probability

Gradients and subgradients are central to optimization and sensitivity analysis of buffered failure probabilities. We furnish a characterization of subgradients based on subdifferential calculus in the case of finite probability distributions and, under additional assumptions, also a gradient expression for general distributions. Several examples illustrate the application of the results, especially in the context of optimality conditions.

Good and Bad Optimization Models: Insights from Rockafellians

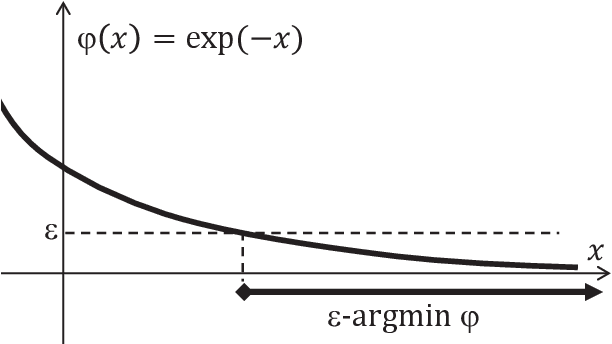
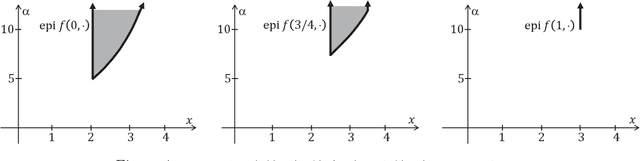
A basic requirement for a mathematical model is often that its solution (output) shouldn't change much if the model's parameters (input) are perturbed. This is important because the exact values of parameters may not be known and one would like to avoid being mislead by an output obtained using incorrect values. Thus, it's rarely enough to address an application by formulating a model, solving the resulting optimization problem and presenting the solution as the answer. One would need to confirm that the model is suitable, i.e., "good," and this can, at least in part, be achieved by considering a family of optimization problems constructed by perturbing parameters of concern. The resulting sensitivity analysis uncovers troubling situations with unstable solutions, which we referred to as "bad" models, and indicates better model formulations. Embedding an actual problem of interest within a family of problems is also a primary path to optimality conditions as well as computationally attractive, alternative problems, which under ideal circumstances, and when properly tuned, may even furnish the minimum value of the actual problem. The tuning of these alternative problems turns out to be intimately tied to finding multipliers in optimality conditions and thus emerges as a main component of several optimization algorithms. In fact, the tuning amounts to solving certain dual optimization problems. In this tutorial, we'll discuss the opportunities and insights afforded by this broad perspective.

Diametrical Risk Minimization: Theory and Computations

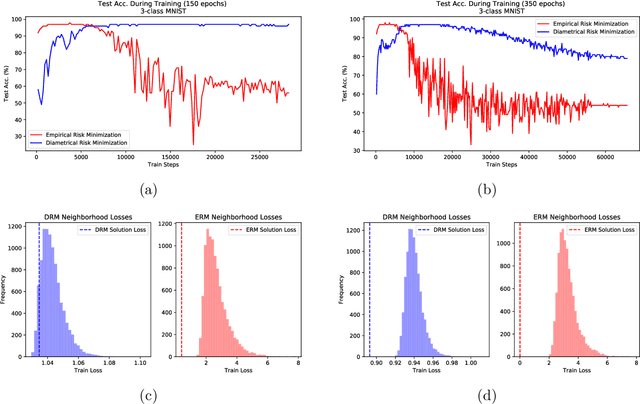
The theoretical and empirical performance of Empirical Risk Minimization (ERM) often suffers when loss functions are poorly behaved with large Lipschitz moduli and spurious sharp minimizers. We propose and analyze a counterpart to ERM called Diametrical Risk Minimization (DRM), which accounts for worst-case empirical risks within neighborhoods in parameter space. DRM has generalization bounds that are independent of Lipschitz moduli for convex as well as nonconvex problems and it can be implemented using a practical algorithm based on stochastic gradient descent. Numerical results illustrate the ability of DRM to find quality solutions with low generalization error in chaotic landscapes from benchmark neural network classification problems with corrupted labels.