Diametrical Risk Minimization: Theory and Computations

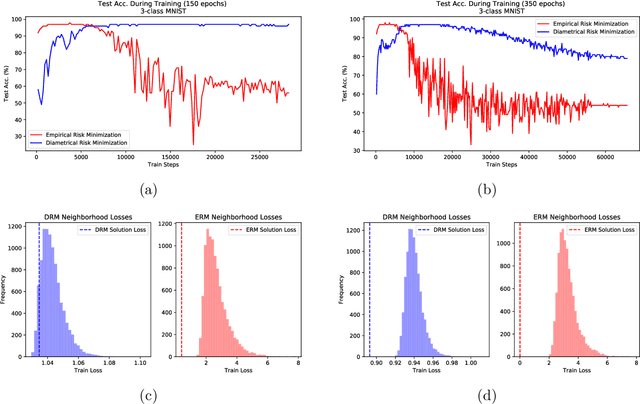
The theoretical and empirical performance of Empirical Risk Minimization (ERM) often suffers when loss functions are poorly behaved with large Lipschitz moduli and spurious sharp minimizers. We propose and analyze a counterpart to ERM called Diametrical Risk Minimization (DRM), which accounts for worst-case empirical risks within neighborhoods in parameter space. DRM has generalization bounds that are independent of Lipschitz moduli for convex as well as nonconvex problems and it can be implemented using a practical algorithm based on stochastic gradient descent. Numerical results illustrate the ability of DRM to find quality solutions with low generalization error in chaotic landscapes from benchmark neural network classification problems with corrupted labels.

Generalized Batch Normalization: Towards Accelerating Deep Neural Networks

Utilizing recently introduced concepts from statistics and quantitative risk management, we present a general variant of Batch Normalization (BN) that offers accelerated convergence of Neural Network training compared to conventional BN. In general, we show that mean and standard deviation are not always the most appropriate choice for the centering and scaling procedure within the BN transformation, particularly if ReLU follows the normalization step. We present a Generalized Batch Normalization (GBN) transformation, which can utilize a variety of alternative deviation measures for scaling and statistics for centering, choices which naturally arise from the theory of generalized deviation measures and risk theory in general. When used in conjunction with the ReLU non-linearity, the underlying risk theory suggests natural, arguably optimal choices for the deviation measure and statistic. Utilizing the suggested deviation measure and statistic, we show experimentally that training is accelerated more so than with conventional BN, often with improved error rate as well. Overall, we propose a more flexible BN transformation supported by a complimentary theoretical framework that can potentially guide design choices.

Optimistic Robust Optimization With Applications To Machine Learning

Robust Optimization has traditionally taken a pessimistic, or worst-case viewpoint of uncertainty which is motivated by a desire to find sets of optimal policies that maintain feasibility under a variety of operating conditions. In this paper, we explore an optimistic, or best-case view of uncertainty and show that it can be a fruitful approach. We show that these techniques can be used to address a wide variety of problems. First, we apply our methods in the context of robust linear programming, providing a method for reducing conservatism in intuitive ways that encode economically realistic modeling assumptions. Second, we look at problems in machine learning and find that this approach is strongly connected to the existing literature. Specifically, we provide a new interpretation for popular sparsity inducing non-convex regularization schemes. Additionally, we show that successful approaches for dealing with outliers and noise can be interpreted as optimistic robust optimization problems. Although many of the problems resulting from our approach are non-convex, we find that DCA or DCA-like optimization approaches can be intuitive and efficient.