Diametrical Risk Minimization: Theory and Computations

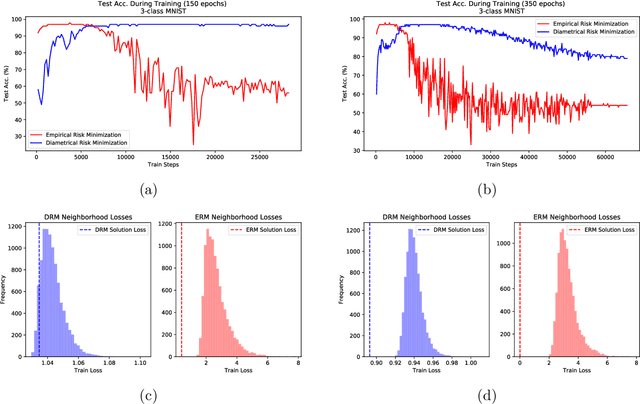
The theoretical and empirical performance of Empirical Risk Minimization (ERM) often suffers when loss functions are poorly behaved with large Lipschitz moduli and spurious sharp minimizers. We propose and analyze a counterpart to ERM called Diametrical Risk Minimization (DRM), which accounts for worst-case empirical risks within neighborhoods in parameter space. DRM has generalization bounds that are independent of Lipschitz moduli for convex as well as nonconvex problems and it can be implemented using a practical algorithm based on stochastic gradient descent. Numerical results illustrate the ability of DRM to find quality solutions with low generalization error in chaotic landscapes from benchmark neural network classification problems with corrupted labels.