Johannes Lutzeyer
SHAKE-GNN: Scalable Hierarchical Kirchhoff-Forest Graph Neural Network
Sep 26, 2025Abstract:Graph Neural Networks (GNNs) have achieved remarkable success across a range of learning tasks. However, scaling GNNs to large graphs remains a significant challenge, especially for graph-level tasks. In this work, we introduce SHAKE-GNN, a novel scalable graph-level GNN framework based on a hierarchy of Kirchhoff Forests, a class of random spanning forests used to construct stochastic multi-resolution decompositions of graphs. SHAKE-GNN produces multi-scale representations, enabling flexible trade-offs between efficiency and performance. We introduce an improved, data-driven strategy for selecting the trade-off parameter and analyse the time-complexity of SHAKE-GNN. Experimental results on multiple large-scale graph classification benchmarks demonstrate that SHAKE-GNN achieves competitive performance while offering improved scalability.
Efficient Data Selection for Training Genomic Perturbation Models
Mar 18, 2025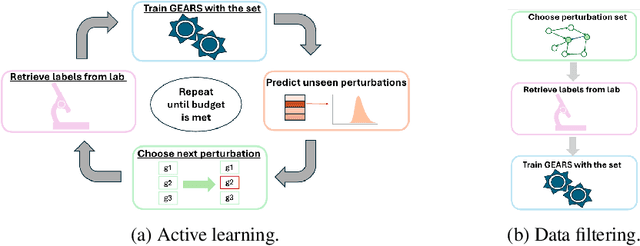
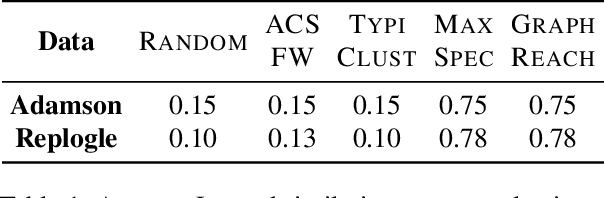
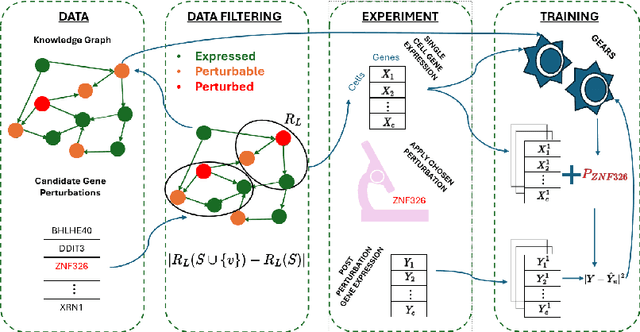
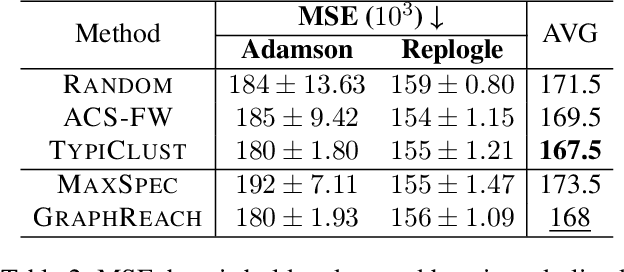
Abstract:Genomic studies, including CRISPR-based PerturbSeq analyses, face a vast hypothesis space, while gene perturbations remain costly and time-consuming. Gene expression models based on graph neural networks are trained to predict the outcomes of gene perturbations to facilitate such experiments. Active learning methods are often employed to train these models due to the cost of the genomic experiments required to build the training set. However, poor model initialization in active learning can result in suboptimal early selections, wasting time and valuable resources. While typical active learning mitigates this issue over many iterations, the limited number of experimental cycles in genomic studies exacerbates the risk. To this end, we propose graph-based one-shot data selection methods for training gene expression models. Unlike active learning, one-shot data selection predefines the gene perturbations before training, hence removing the initialization bias. The data selection is motivated by theoretical studies of graph neural network generalization. The criteria are defined over the input graph and are optimized with submodular maximization. We compare them empirically to baselines and active learning methods that are state-of-the-art on this problem. The results demonstrate that graph-based one-shot data selection achieves comparable accuracy while alleviating the aforementioned risks.
Graph Neural Machine: A New Model for Learning with Tabular Data
Feb 05, 2024



Abstract:In recent years, there has been a growing interest in mapping data from different domains to graph structures. Among others, neural network models such as the multi-layer perceptron (MLP) can be modeled as graphs. In fact, MLPs can be represented as directed acyclic graphs. Graph neural networks (GNNs) have recently become the standard tool for performing machine learning tasks on graphs. In this work, we show that an MLP is equivalent to an asynchronous message passing GNN model which operates on the MLP's graph representation. We then propose a new machine learning model for tabular data, the so-called Graph Neural Machine (GNM), which replaces the MLP's directed acyclic graph with a nearly complete graph and which employs a synchronous message passing scheme. We show that a single GNM model can simulate multiple MLP models. We evaluate the proposed model in several classification and regression datasets. In most cases, the GNM model outperforms the MLP architecture.
Path Neural Networks: Expressive and Accurate Graph Neural Networks
Jun 09, 2023



Abstract:Graph neural networks (GNNs) have recently become the standard approach for learning with graph-structured data. Prior work has shed light into their potential, but also their limitations. Unfortunately, it was shown that standard GNNs are limited in their expressive power. These models are no more powerful than the 1-dimensional Weisfeiler-Leman (1-WL) algorithm in terms of distinguishing non-isomorphic graphs. In this paper, we propose Path Neural Networks (PathNNs), a model that updates node representations by aggregating paths emanating from nodes. We derive three different variants of the PathNN model that aggregate single shortest paths, all shortest paths and all simple paths of length up to K. We prove that two of these variants are strictly more powerful than the 1-WL algorithm, and we experimentally validate our theoretical results. We find that PathNNs can distinguish pairs of non-isomorphic graphs that are indistinguishable by 1-WL, while our most expressive PathNN variant can even distinguish between 3-WL indistinguishable graphs. The different PathNN variants are also evaluated on graph classification and graph regression datasets, where in most cases, they outperform the baseline methods.
How the Move Acceptance Hyper-Heuristic Copes With Local Optima: Drastic Differences Between Jumps and Cliffs
Apr 20, 2023Abstract:In recent work, Lissovoi, Oliveto, and Warwicker (Artificial Intelligence (2023)) proved that the Move Acceptance Hyper-Heuristic (MAHH) leaves the local optimum of the multimodal cliff benchmark with remarkable efficiency. With its $O(n^3)$ runtime, for almost all cliff widths $d,$ the MAHH massively outperforms the $\Theta(n^d)$ runtime of simple elitist evolutionary algorithms (EAs). For the most prominent multimodal benchmark, the jump functions, the given runtime estimates of $O(n^{2m} m^{-\Theta(m)})$ and $\Omega(2^{\Omega(m)})$, for gap size $m \ge 2$, are far apart and the real performance of MAHH is still an open question. In this work, we resolve this question. We prove that for any choice of the MAHH selection parameter~$p$, the expected runtime of the MAHH on a jump function with gap size $m = o(n^{1/2})$ is at least $\Omega(n^{2m-1} / (2m-1)!)$. This renders the MAHH much slower than simple elitist evolutionary algorithms with their typical $O(n^m)$ runtime. We also show that the MAHH with the global bit-wise mutation operator instead of the local one-bit operator optimizes jump functions in time $O(\min\{m n^m,\frac{n^{2m-1}}{m!\Omega(m)^{m-2}}\})$, essentially the minimum of the optimization times of the $(1+1)$ EA and the MAHH. This suggests that combining several ways to cope with local optima can be a fruitful approach.
Learning Parametrised Graph Shift Operators
Jan 25, 2021



Abstract:In many domains data is currently represented as graphs and therefore, the graph representation of this data becomes increasingly important in machine learning. Network data is, implicitly or explicitly, always represented using a graph shift operator (GSO) with the most common choices being the adjacency, Laplacian matrices and their normalisations. In this paper, a novel parametrised GSO (PGSO) is proposed, where specific parameter values result in the most commonly used GSOs and message-passing operators in graph neural network (GNN) frameworks. The PGSO is suggested as a replacement of the standard GSOs that are used in state-of-the-art GNN architectures and the optimisation of the PGSO parameters is seamlessly included in the model training. It is proved that the PGSO has real eigenvalues and a set of real eigenvectors independent of the parameter values and spectral bounds on the PGSO are derived. PGSO parameters are shown to adapt to the sparsity of the graph structure in a study on stochastic blockmodel networks, where they are found to automatically replicate the GSO regularisation found in the literature. On several real-world datasets the accuracy of state-of-the-art GNN architectures is improved by the inclusion of the PGSO in both node- and graph-classification tasks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge