Pattern representation and recognition with accelerated analog neuromorphic systems

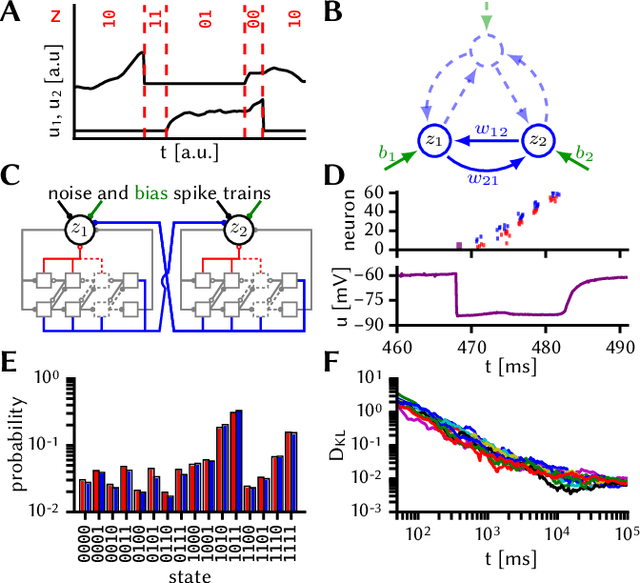
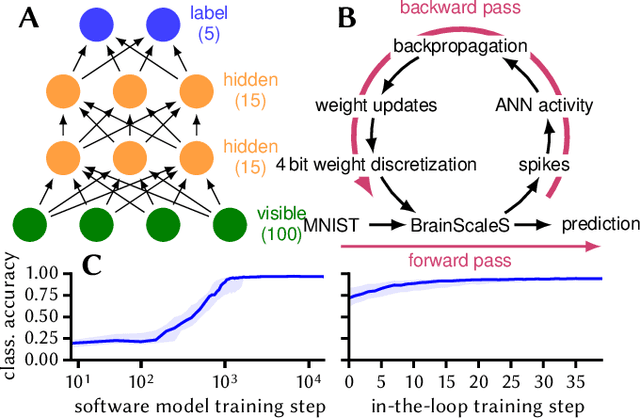
Despite being originally inspired by the central nervous system, artificial neural networks have diverged from their biological archetypes as they have been remodeled to fit particular tasks. In this paper, we review several possibilites to reverse map these architectures to biologically more realistic spiking networks with the aim of emulating them on fast, low-power neuromorphic hardware. Since many of these devices employ analog components, which cannot be perfectly controlled, finding ways to compensate for the resulting effects represents a key challenge. Here, we discuss three different strategies to address this problem: the addition of auxiliary network components for stabilizing activity, the utilization of inherently robust architectures and a training method for hardware-emulated networks that functions without perfect knowledge of the system's dynamics and parameters. For all three scenarios, we corroborate our theoretical considerations with experimental results on accelerated analog neuromorphic platforms.

Stochastic inference with spiking neurons in the high-conductance state

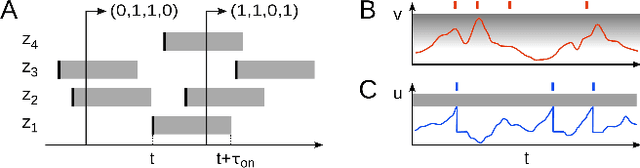
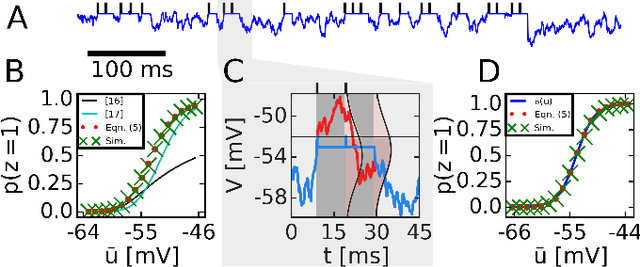
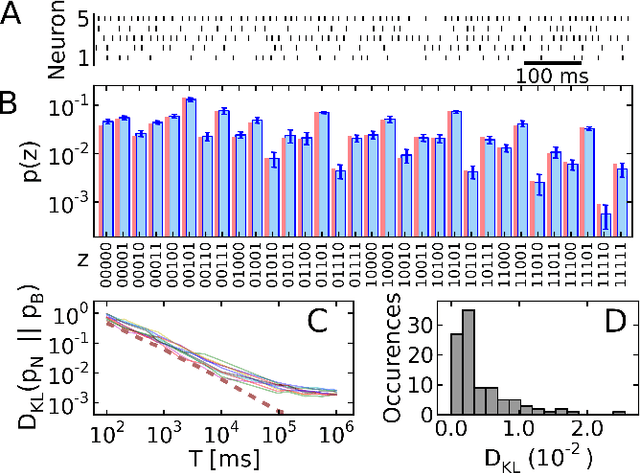
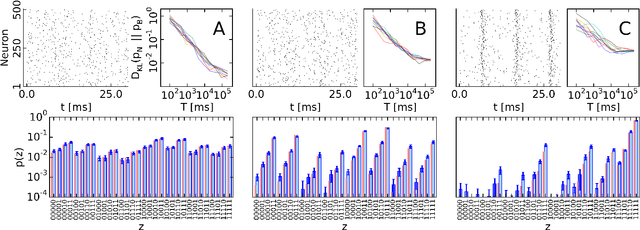
The highly variable dynamics of neocortical circuits observed in vivo have been hypothesized to represent a signature of ongoing stochastic inference but stand in apparent contrast to the deterministic response of neurons measured in vitro. Based on a propagation of the membrane autocorrelation across spike bursts, we provide an analytical derivation of the neural activation function that holds for a large parameter space, including the high-conductance state. On this basis, we show how an ensemble of leaky integrate-and-fire neurons with conductance-based synapses embedded in a spiking environment can attain the correct firing statistics for sampling from a well-defined target distribution. For recurrent networks, we examine convergence toward stationarity in computer simulations and demonstrate sample-based Bayesian inference in a mixed graphical model. This points to a new computational role of high-conductance states and establishes a rigorous link between deterministic neuron models and functional stochastic dynamics on the network level.

The high-conductance state enables neural sampling in networks of LIF neurons

The apparent stochasticity of in-vivo neural circuits has long been hypothesized to represent a signature of ongoing stochastic inference in the brain. More recently, a theoretical framework for neural sampling has been proposed, which explains how sample-based inference can be performed by networks of spiking neurons. One particular requirement of this approach is that the neural response function closely follows a logistic curve. Analytical approaches to calculating neural response functions have been the subject of many theoretical studies. In order to make the problem tractable, particular assumptions regarding the neural or synaptic parameters are usually made. However, biologically significant activity regimes exist which are not covered by these approaches: Under strong synaptic bombardment, as is often the case in cortex, the neuron is shifted into a high-conductance state (HCS) characterized by a small membrane time constant. In this regime, synaptic time constants and refractory periods dominate membrane dynamics. The core idea of our approach is to separately consider two different "modes" of spiking dynamics: burst spiking and transient quiescence, in which the neuron does not spike for longer periods. We treat the former by propagating the PDF of the effective membrane potential from spike to spike within a burst, while using a diffusion approximation for the latter. We find that our prediction of the neural response function closely matches simulation data. Moreover, in the HCS scenario, we show that the neural response function becomes symmetric and can be well approximated by a logistic function, thereby providing the correct dynamics in order to perform neural sampling. We hereby provide not only a normative framework for Bayesian inference in cortex, but also powerful applications of low-power, accelerated neuromorphic systems to relevant machine learning tasks.

Stochastic inference with deterministic spiking neurons

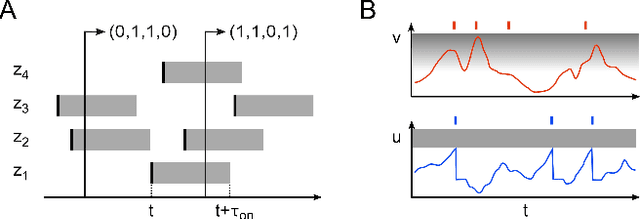
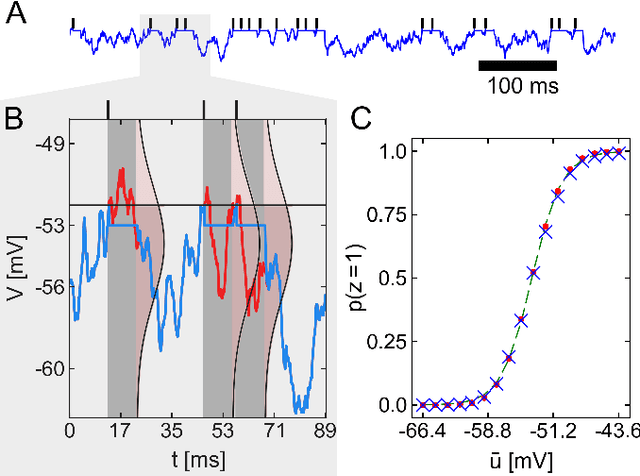
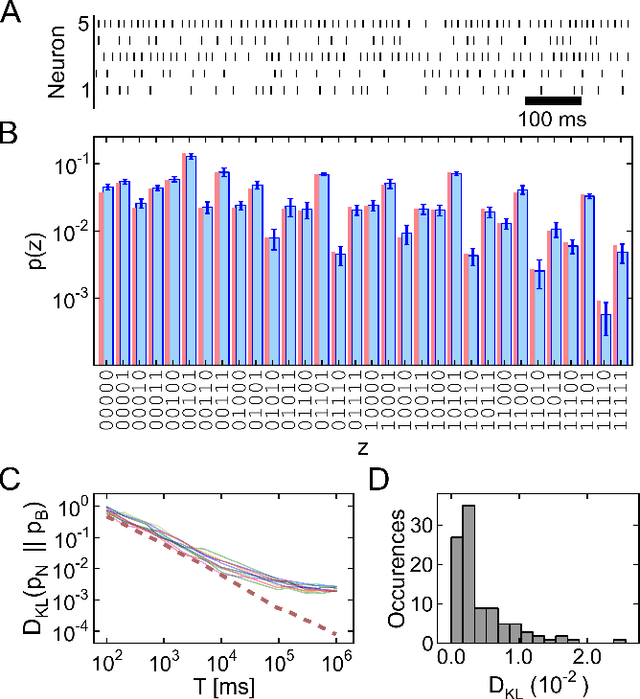
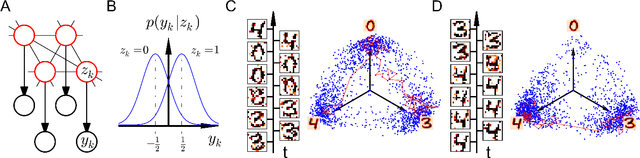
The seemingly stochastic transient dynamics of neocortical circuits observed in vivo have been hypothesized to represent a signature of ongoing stochastic inference. In vitro neurons, on the other hand, exhibit a highly deterministic response to various types of stimulation. We show that an ensemble of deterministic leaky integrate-and-fire neurons embedded in a spiking noisy environment can attain the correct firing statistics in order to sample from a well-defined target distribution. We provide an analytical derivation of the activation function on the single cell level; for recurrent networks, we examine convergence towards stationarity in computer simulations and demonstrate sample-based Bayesian inference in a mixed graphical model. This establishes a rigorous link between deterministic neuron models and functional stochastic dynamics on the network level.