ReviBranch: Deep Reinforcement Learning for Branch-and-Bound with Revived Trajectories

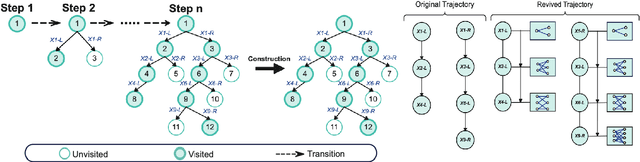
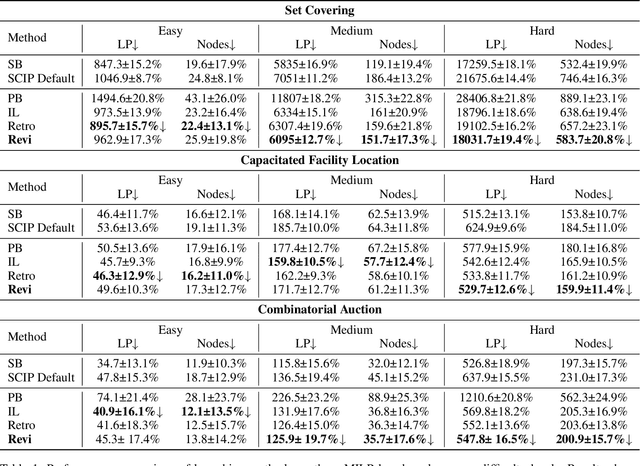
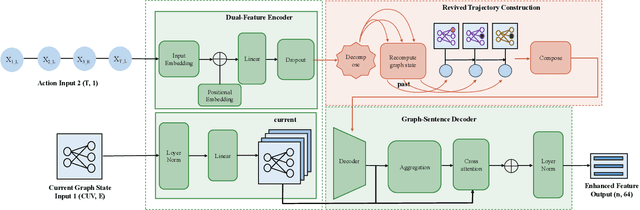
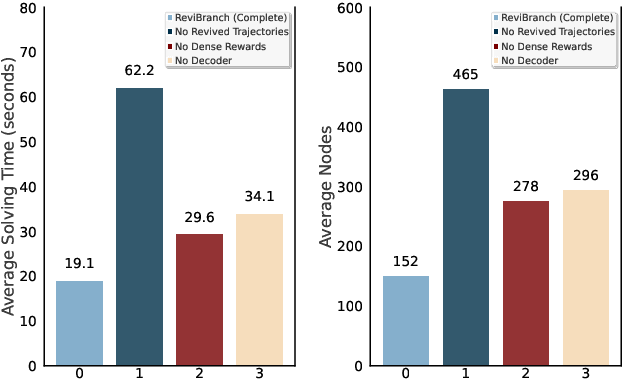
The Branch-and-bound (B&B) algorithm is the main solver for Mixed Integer Linear Programs (MILPs), where the selection of branching variable is essential to computational efficiency. However, traditional heuristics for branching often fail to generalize across heterogeneous problem instances, while existing learning-based methods such as imitation learning (IL) suffers from dependence on expert demonstration quality, and reinforcement learning (RL) struggles with limitations in sparse rewards and dynamic state representation challenges. To address these issues, we propose ReviBranch, a novel deep RL framework that constructs revived trajectories by reviving explicit historical correspondences between branching decisions and their corresponding graph states along search-tree paths. During training, ReviBranch enables agents to learn from complete structural evolution and temporal dependencies within the branching process. Additionally, we introduce an importance-weighted reward redistribution mechanism that transforms sparse terminal rewards into dense stepwise feedback, addressing the sparse reward challenge. Extensive experiments on different MILP benchmarks demonstrate that ReviBranch outperforms state-of-the-art RL methods, reducing B&B nodes by 4.0% and LP iterations by 2.2% on large-scale instances. The results highlight the robustness and generalizability of ReviBranch across heterogeneous MILP problem classes.

PIONM: A Generalized Approach to Solving Density-Constrained Mean-Field Games Equilibrium under Modified Boundary Conditions

Neural network-based methods are effective for solving equilibria in Mean-Field Games (MFGs), particularly in high-dimensional settings. However, solving the coupled partial differential equations (PDEs) in MFGs limits their applicability since solving coupled PDEs is computationally expensive. Additionally, modifying boundary conditions, such as the initial state distribution or terminal value function, necessitates extensive retraining, reducing scalability. To address these challenges, we propose a generalized framework, PIONM (Physics-Informed Neural Operator NF-MKV Net), which leverages physics-informed neural operators to solve MFGs equations. PIONM utilizes neural operators to compute MFGs equilibria for arbitrary boundary conditions. The method encodes boundary conditions as input features and trains the model to align them with density evolution, modeled using discrete-time normalizing flows. Once trained, the algorithm efficiently computes the density distribution at any time step for modified boundary condition, ensuring efficient adaptation to different boundary conditions in MFGs equilibria. Unlike traditional MFGs methods constrained by fixed coefficients, PIONM efficiently computes equilibria under varying boundary conditions, including obstacles, diffusion coefficients, initial densities, and terminal functions. PIONM can adapt to modified conditions while preserving density distribution constraints, demonstrating superior scalability and generalization capabilities compared to existing methods.

NF-MKV Net: A Constraint-Preserving Neural Network Approach to Solving Mean-Field Games Equilibrium

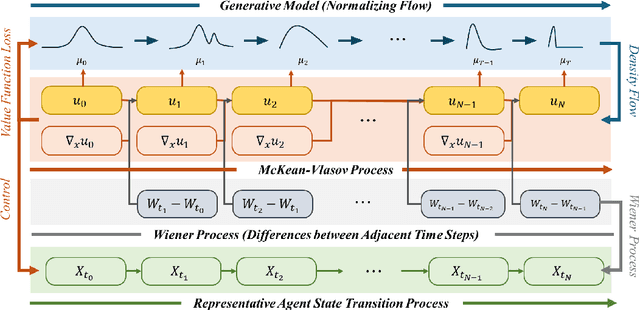
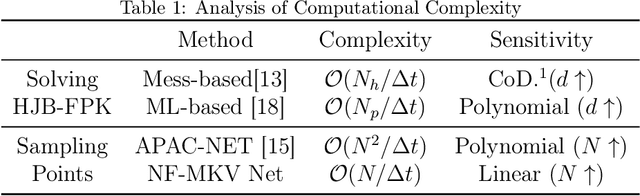
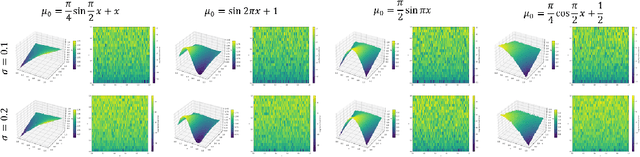
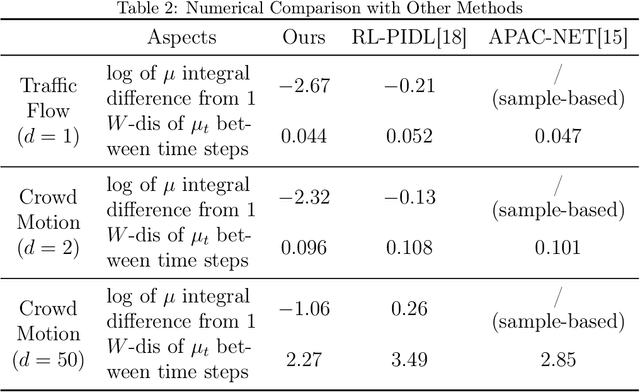
Neural network-based methods for solving Mean-Field Games (MFGs) equilibria have garnered significant attention for their effectiveness in high-dimensional problems. However, many algorithms struggle with ensuring that the evolution of the density distribution adheres to the required mathematical constraints. This paper investigates a neural network approach to solving MFGs equilibria through a stochastic process perspective. It integrates process-regularized Normalizing Flow (NF) frameworks with state-policy-connected time-series neural networks to address McKean-Vlasov-type Forward-Backward Stochastic Differential Equation (MKV FBSDE) fixed-point problems, equivalent to MFGs equilibria.

AgentPose: Progressive Distribution Alignment via Feature Agent for Human Pose Distillation

Pose distillation is widely adopted to reduce model size in human pose estimation. However, existing methods primarily emphasize the transfer of teacher knowledge while often neglecting the performance degradation resulted from the curse of capacity gap between teacher and student. To address this issue, we propose AgentPose, a novel pose distillation method that integrates a feature agent to model the distribution of teacher features and progressively aligns the distribution of student features with that of the teacher feature, effectively overcoming the capacity gap and enhancing the ability of knowledge transfer. Our comprehensive experiments conducted on the COCO dataset substantiate the effectiveness of our method in knowledge transfer, particularly in scenarios with a high capacity gap.