NF-MKV Net: A Constraint-Preserving Neural Network Approach to Solving Mean-Field Games Equilibrium

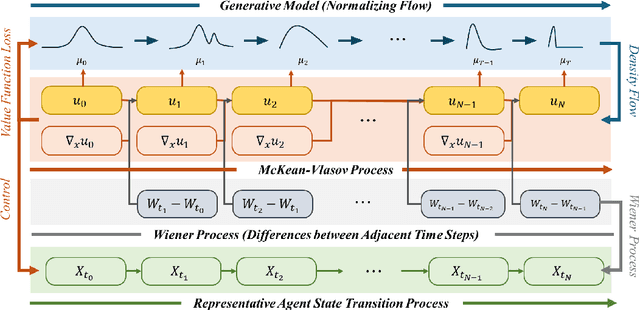
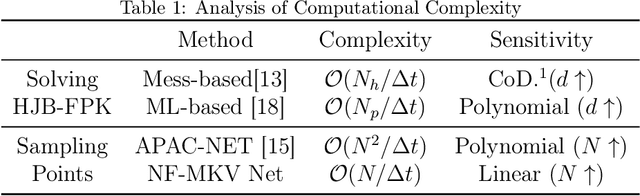
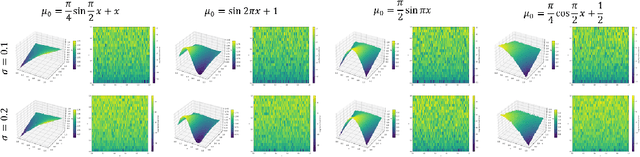
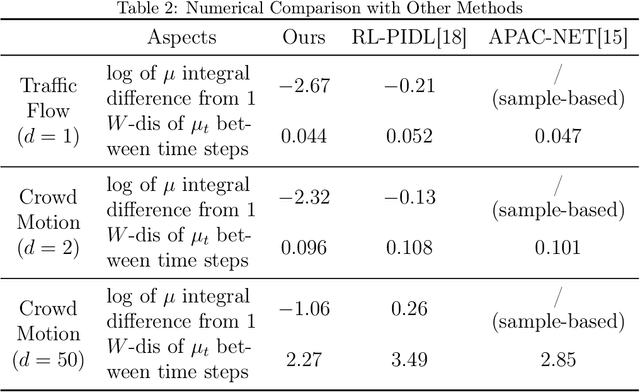
Neural network-based methods for solving Mean-Field Games (MFGs) equilibria have garnered significant attention for their effectiveness in high-dimensional problems. However, many algorithms struggle with ensuring that the evolution of the density distribution adheres to the required mathematical constraints. This paper investigates a neural network approach to solving MFGs equilibria through a stochastic process perspective. It integrates process-regularized Normalizing Flow (NF) frameworks with state-policy-connected time-series neural networks to address McKean-Vlasov-type Forward-Backward Stochastic Differential Equation (MKV FBSDE) fixed-point problems, equivalent to MFGs equilibria.