STL-SGD: Speeding Up Local SGD with Stagewise Communication Period

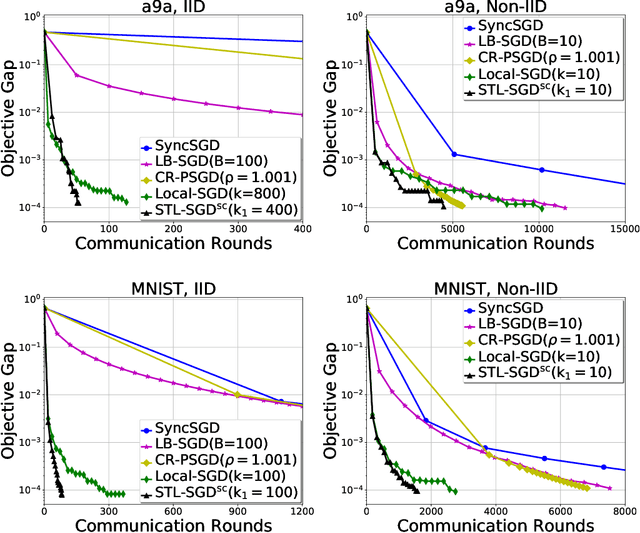
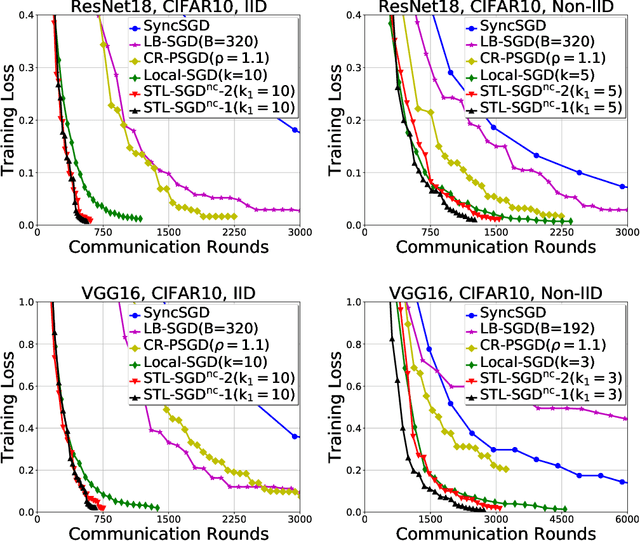
Distributed parallel stochastic gradient descent algorithms are workhorses for large scale machine learning tasks. Among them, local stochastic gradient descent (Local SGD) has attracted significant attention due to its low communication complexity. Previous studies prove that the communication complexity of Local SGD with a fixed or an adaptive communication period is in the order of $O (N^{\frac{3}{2}} T^{\frac{1}{2}})$ and $O (N^{\frac{3}{4}} T^{\frac{3}{4}})$ when the data distributions on clients are identical (IID) or otherwise (Non-IID). In this paper, to accelerate the convergence by reducing the communication complexity, we propose \textit{ST}agewise \textit{L}ocal \textit{SGD} (STL-SGD), which increases the communication period gradually along with decreasing learning rate. We prove that STL-SGD can keep the same convergence rate and linear speedup as mini-batch SGD. In addition, as the benefit of increasing the communication period, when the objective is strongly convex or satisfies the Polyak-\L ojasiewicz condition, the communication complexity of STL-SGD is $O (N \log{T})$ and $O (N^{\frac{1}{2}} T^{\frac{1}{2}})$ for the IID case and the Non-IID case respectively, achieving significant improvements over Local SGD. Experiments on both convex and non-convex problems demonstrate the superior performance of STL-SGD.

Variance Reduced Local SGD with Lower Communication Complexity

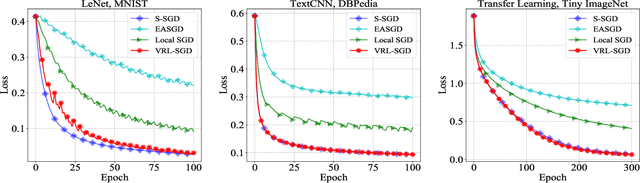
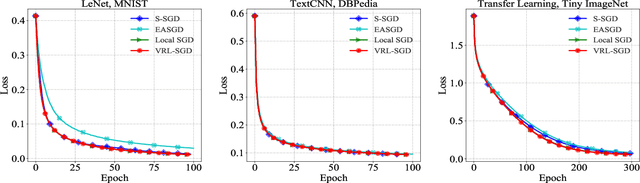
To accelerate the training of machine learning models, distributed stochastic gradient descent (SGD) and its variants have been widely adopted, which apply multiple workers in parallel to speed up training. Among them, Local SGD has gained much attention due to its lower communication cost. Nevertheless, when the data distribution on workers is non-identical, Local SGD requires $O(T^{\frac{3}{4}} N^{\frac{3}{4}})$ communications to maintain its \emph{linear iteration speedup} property, where $T$ is the total number of iterations and $N$ is the number of workers. In this paper, we propose Variance Reduced Local SGD (VRL-SGD) to further reduce the communication complexity. Benefiting from eliminating the dependency on the gradient variance among workers, we theoretically prove that VRL-SGD achieves a \emph{linear iteration speedup} with a lower communication complexity $O(T^{\frac{1}{2}} N^{\frac{3}{2}})$ even if workers access non-identical datasets. We conduct experiments on three machine learning tasks, and the experimental results demonstrate that VRL-SGD performs impressively better than Local SGD when the data among workers are quite diverse.

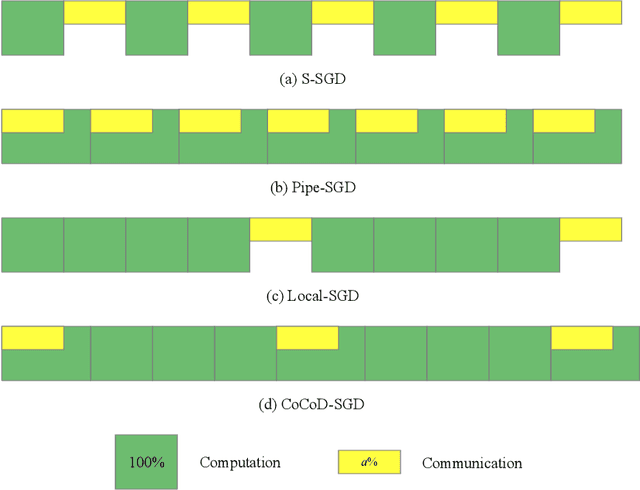
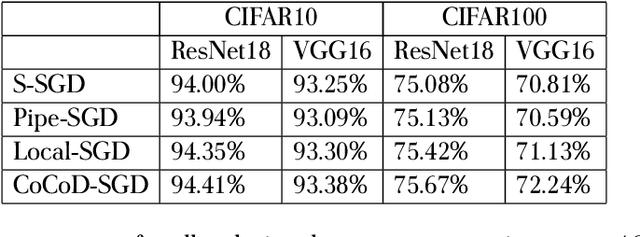
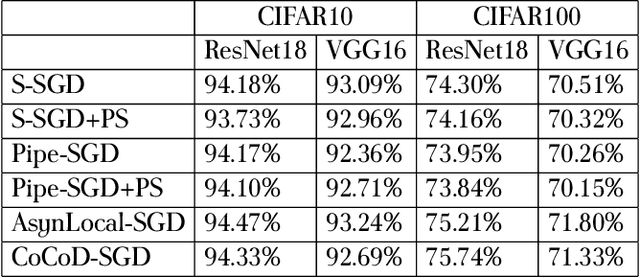
Faster Distributed Deep Net Training: Computation and Communication Decoupled Stochastic Gradient Descent

With the increase in the amount of data and the expansion of model scale, distributed parallel training becomes an important and successful technique to address the optimization challenges. Nevertheless, although distributed stochastic gradient descent (SGD) algorithms can achieve a linear iteration speedup, they are limited significantly in practice by the communication cost, making it difficult to achieve a linear time speedup. In this paper, we propose a computation and communication decoupled stochastic gradient descent (CoCoD-SGD) algorithm to run computation and communication in parallel to reduce the communication cost. We prove that CoCoD-SGD has a linear iteration speedup with respect to the total computation capability of the hardware resources. In addition, it has a lower communication complexity and better time speedup comparing with traditional distributed SGD algorithms. Experiments on deep neural network training demonstrate the significant improvements of CoCoD-SGD: when training ResNet18 and VGG16 with 16 Geforce GTX 1080Ti GPUs, CoCoD-SGD is up to 2-3$\times$ faster than traditional synchronous SGD.

Asynchronous Stochastic Composition Optimization with Variance Reduction

Composition optimization has drawn a lot of attention in a wide variety of machine learning domains from risk management to reinforcement learning. Existing methods solving the composition optimization problem often work in a sequential and single-machine manner, which limits their applications in large-scale problems. To address this issue, this paper proposes two asynchronous parallel variance reduced stochastic compositional gradient (AsyVRSC) algorithms that are suitable to handle large-scale data sets. The two algorithms are AsyVRSC-Shared for the shared-memory architecture and AsyVRSC-Distributed for the master-worker architecture. The embedded variance reduction techniques enable the algorithms to achieve linear convergence rates. Furthermore, AsyVRSC-Shared and AsyVRSC-Distributed enjoy provable linear speedup, when the time delays are bounded by the data dimensionality or the sparsity ratio of the partial gradients, respectively. Extensive experiments are conducted to verify the effectiveness of the proposed algorithms.

Accelerating Stochastic Gradient Descent Using Antithetic Sampling

(Mini-batch) Stochastic Gradient Descent is a popular optimization method which has been applied to many machine learning applications. But a rather high variance introduced by the stochastic gradient in each step may slow down the convergence. In this paper, we propose the antithetic sampling strategy to reduce the variance by taking advantage of the internal structure in dataset. Under this new strategy, stochastic gradients in a mini-batch are no longer independent but negatively correlated as much as possible, while the mini-batch stochastic gradient is still an unbiased estimator of full gradient. For the binary classification problems, we just need to calculate the antithetic samples in advance, and reuse the result in each iteration, which is practical. Experiments are provided to confirm the effectiveness of the proposed method.