Variance Reduced Local SGD with Lower Communication Complexity
Paper and Code
Dec 30, 2019
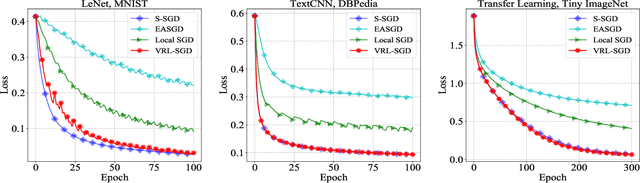

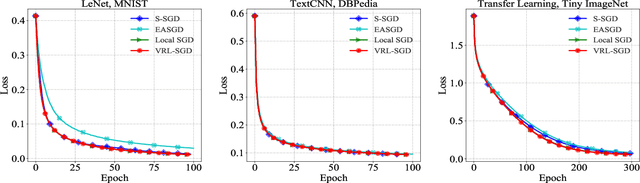
To accelerate the training of machine learning models, distributed stochastic gradient descent (SGD) and its variants have been widely adopted, which apply multiple workers in parallel to speed up training. Among them, Local SGD has gained much attention due to its lower communication cost. Nevertheless, when the data distribution on workers is non-identical, Local SGD requires $O(T^{\frac{3}{4}} N^{\frac{3}{4}})$ communications to maintain its \emph{linear iteration speedup} property, where $T$ is the total number of iterations and $N$ is the number of workers. In this paper, we propose Variance Reduced Local SGD (VRL-SGD) to further reduce the communication complexity. Benefiting from eliminating the dependency on the gradient variance among workers, we theoretically prove that VRL-SGD achieves a \emph{linear iteration speedup} with a lower communication complexity $O(T^{\frac{1}{2}} N^{\frac{3}{2}})$ even if workers access non-identical datasets. We conduct experiments on three machine learning tasks, and the experimental results demonstrate that VRL-SGD performs impressively better than Local SGD when the data among workers are quite diverse.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge