Numerical Approximation of Partial Differential Equations by a Variable Projection Method with Artificial Neural Networks

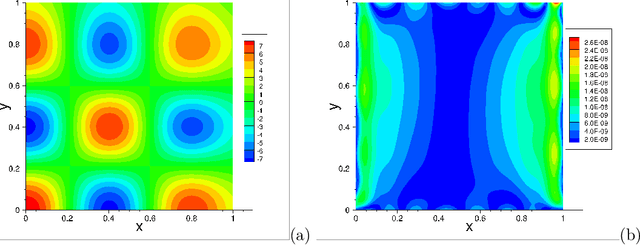
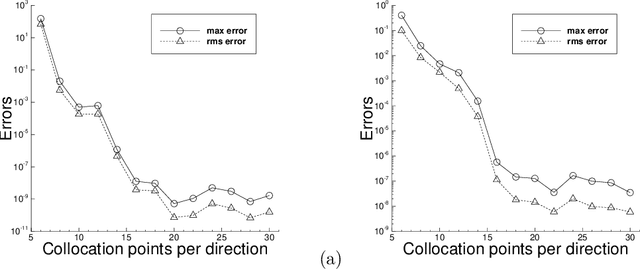
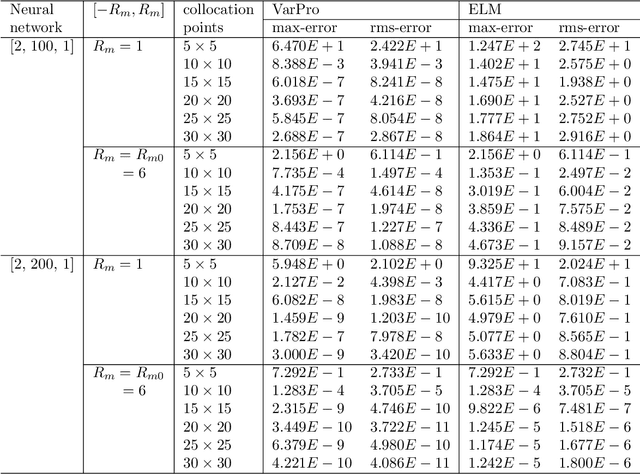
We present a method for solving linear and nonlinear PDEs based on the variable projection (VarPro) framework and artificial neural networks (ANN). For linear PDEs, enforcing the boundary/initial value problem on the collocation points leads to a separable nonlinear least squares problem about the network coefficients. We reformulate this problem by the VarPro approach to eliminate the linear output-layer coefficients, leading to a reduced problem about the hidden-layer coefficients only. The reduced problem is solved first by the nonlinear least squares method to determine the hidden-layer coefficients, and then the output-layer coefficients are computed by the linear least squares method. For nonlinear PDEs, enforcing the boundary/initial value problem on the collocation points leads to a nonlinear least squares problem that is not separable, which precludes the VarPro strategy for such problems. To enable the VarPro approach for nonlinear PDEs, we first linearize the problem with a Newton iteration, using a particular form of linearization. The linearized system is solved by the VarPro framework together with ANNs. Upon convergence of the Newton iteration, the network coefficients provide the representation of the solution field to the original nonlinear problem. We present ample numerical examples with linear and nonlinear PDEs to demonstrate the performance of the method herein. For smooth field solutions, the errors of the current method decrease exponentially as the number of collocation points or the number of output-layer coefficients increases. We compare the current method with the ELM method from a previous work. Under identical conditions and network configurations, the current method exhibits an accuracy significantly superior to the ELM method.

On Computing the Hyperparameter of Extreme Learning Machines: Algorithm and Application to Computational PDEs, and Comparison with Classical and High-Order Finite Elements

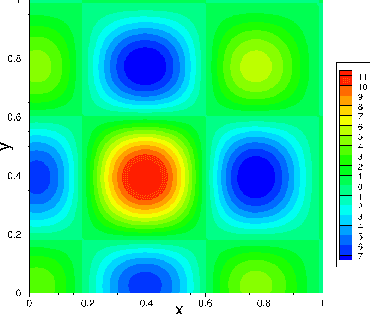
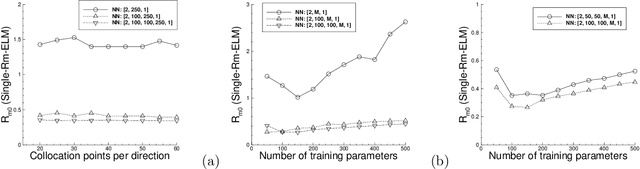
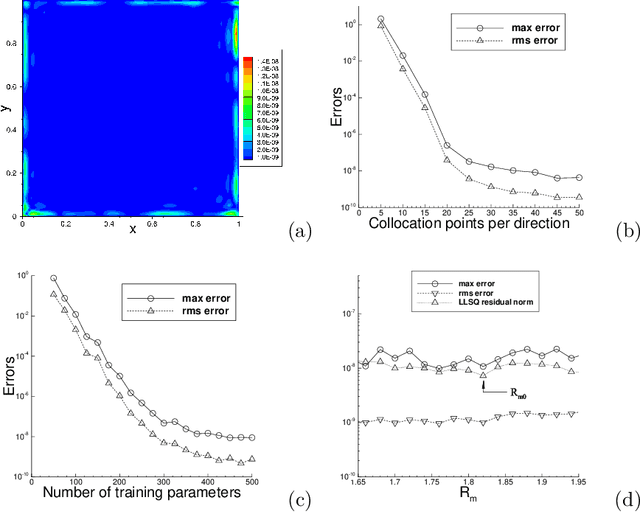
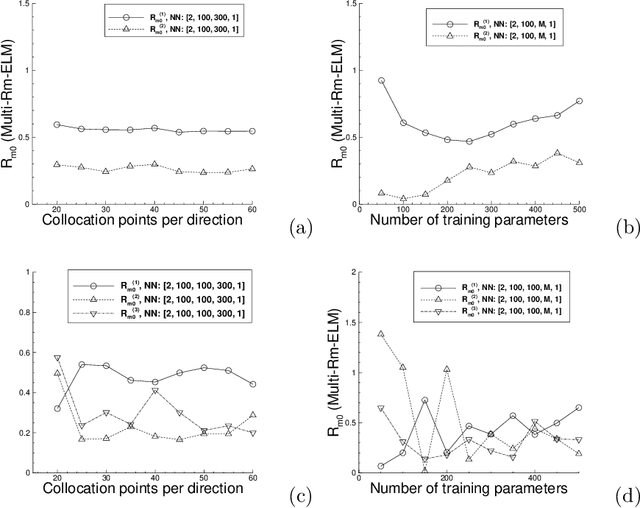
We consider the use of extreme learning machines (ELM) for computational partial differential equations (PDE). In ELM the hidden-layer coefficients in the neural network are assigned to random values generated on $[-R_m,R_m]$ and fixed, where $R_m$ is a user-provided constant, and the output-layer coefficients are trained by a linear or nonlinear least squares computation. We present a method for computing the optimal value of $R_m$ based on the differential evolution algorithm. The presented method enables us to illuminate the characteristics of the optimal $R_m$ for two types of ELM configurations: (i) Single-Rm-ELM, in which a single $R_m$ is used for generating the random coefficients in all the hidden layers, and (ii) Multi-Rm-ELM, in which multiple $R_m$ constants are involved with each used for generating the random coefficients of a different hidden layer. We adopt the optimal $R_m$ from this method and also incorporate other improvements into the ELM implementation. In particular, here we compute all the differential operators involving the output fields of the last hidden layer by a forward-mode auto-differentiation, as opposed to the reverse-mode auto-differentiation in a previous work. These improvements significantly reduce the network training time and enhance the ELM performance. We systematically compare the computational performance of the current improved ELM with that of the finite element method (FEM), both the classical second-order FEM and the high-order FEM with Lagrange elements of higher degrees, for solving a number of linear and nonlinear PDEs. It is shown that the current improved ELM far outperforms the classical FEM. Its computational performance is comparable to that of the high-order FEM for smaller problem sizes, and for larger problem sizes the ELM markedly outperforms the high-order FEM.

Protecting Big Data Privacy Using Randomized Tensor Network Decomposition and Dispersed Tensor Computation

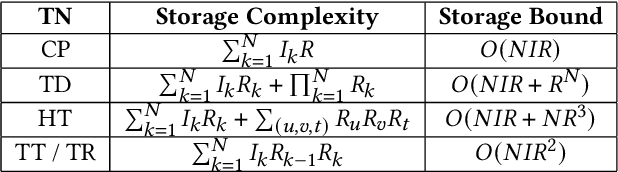
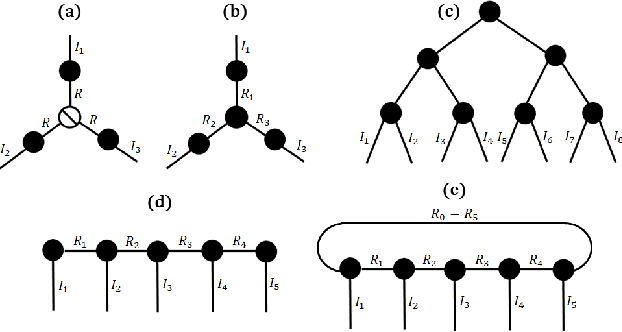
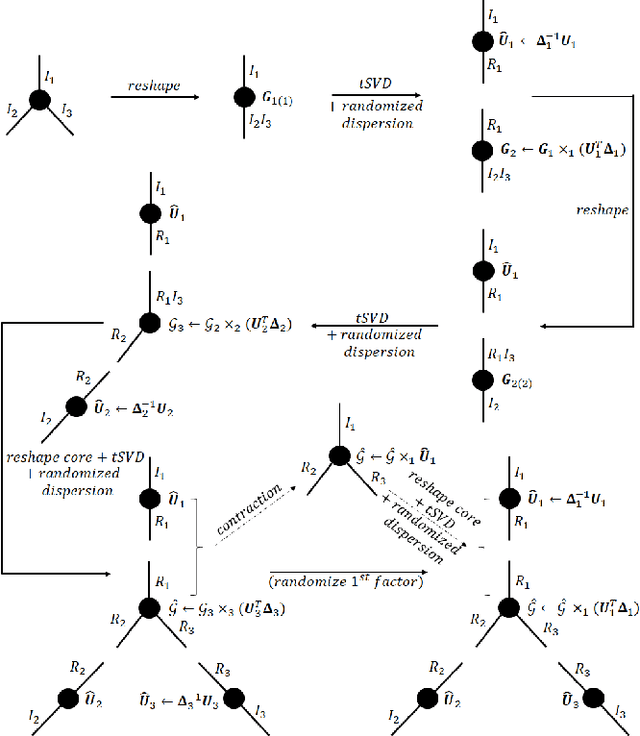
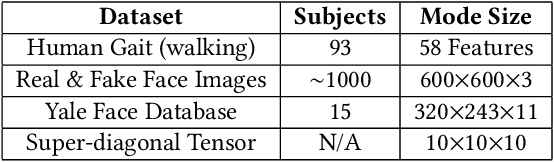
Data privacy is an important issue for organizations and enterprises to securely outsource data storage, sharing, and computation on clouds / fogs. However, data encryption is complicated in terms of the key management and distribution; existing secure computation techniques are expensive in terms of computational / communication cost and therefore do not scale to big data computation. Tensor network decomposition and distributed tensor computation have been widely used in signal processing and machine learning for dimensionality reduction and large-scale optimization. However, the potential of distributed tensor networks for big data privacy preservation have not been considered before, this motivates the current study. Our primary intuition is that tensor network representations are mathematically non-unique, unlinkable, and uninterpretable; tensor network representations naturally support a range of multilinear operations for compressed and distributed / dispersed computation. Therefore, we propose randomized algorithms to decompose big data into randomized tensor network representations and analyze the privacy leakage for 1D to 3D data tensors. The randomness mainly comes from the complex structural information commonly found in big data; randomization is based on controlled perturbation applied to the tensor blocks prior to decomposition. The distributed tensor representations are dispersed on multiple clouds / fogs or servers / devices with metadata privacy, this provides both distributed trust and management to seamlessly secure big data storage, communication, sharing, and computation. Experiments show that the proposed randomization techniques are helpful for big data anonymization and efficient for big data storage and computation.