Numerical Approximation of Partial Differential Equations by a Variable Projection Method with Artificial Neural Networks
Paper and Code
Jan 24, 2022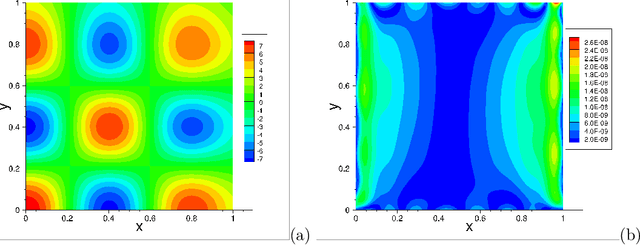

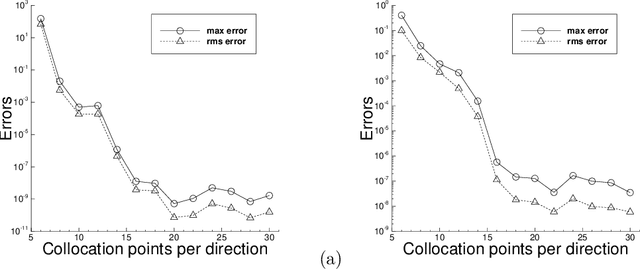
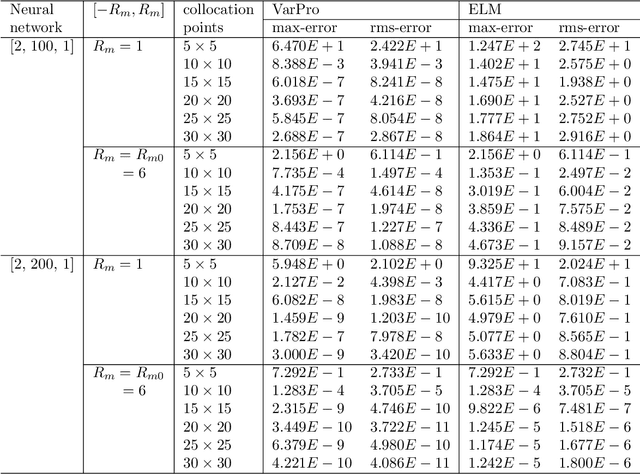
We present a method for solving linear and nonlinear PDEs based on the variable projection (VarPro) framework and artificial neural networks (ANN). For linear PDEs, enforcing the boundary/initial value problem on the collocation points leads to a separable nonlinear least squares problem about the network coefficients. We reformulate this problem by the VarPro approach to eliminate the linear output-layer coefficients, leading to a reduced problem about the hidden-layer coefficients only. The reduced problem is solved first by the nonlinear least squares method to determine the hidden-layer coefficients, and then the output-layer coefficients are computed by the linear least squares method. For nonlinear PDEs, enforcing the boundary/initial value problem on the collocation points leads to a nonlinear least squares problem that is not separable, which precludes the VarPro strategy for such problems. To enable the VarPro approach for nonlinear PDEs, we first linearize the problem with a Newton iteration, using a particular form of linearization. The linearized system is solved by the VarPro framework together with ANNs. Upon convergence of the Newton iteration, the network coefficients provide the representation of the solution field to the original nonlinear problem. We present ample numerical examples with linear and nonlinear PDEs to demonstrate the performance of the method herein. For smooth field solutions, the errors of the current method decrease exponentially as the number of collocation points or the number of output-layer coefficients increases. We compare the current method with the ELM method from a previous work. Under identical conditions and network configurations, the current method exhibits an accuracy significantly superior to the ELM method.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge