On Computing the Hyperparameter of Extreme Learning Machines: Algorithm and Application to Computational PDEs, and Comparison with Classical and High-Order Finite Elements
Paper and Code
Oct 27, 2021
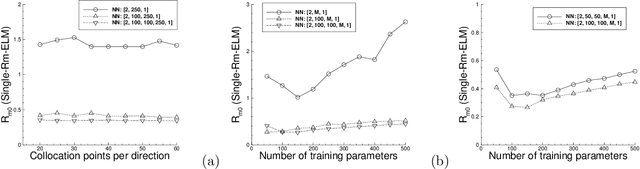
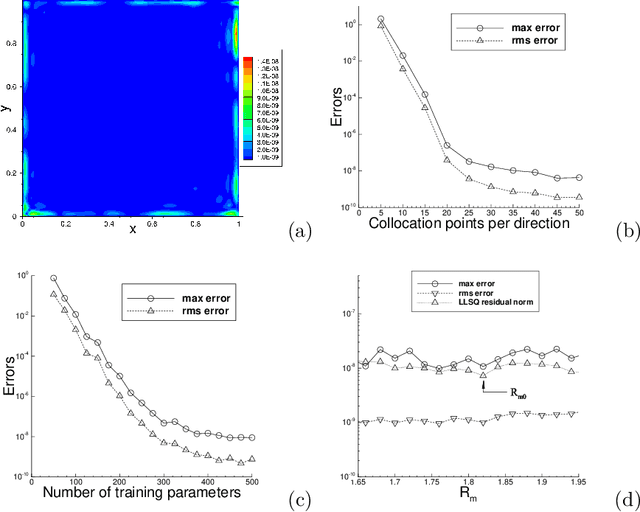
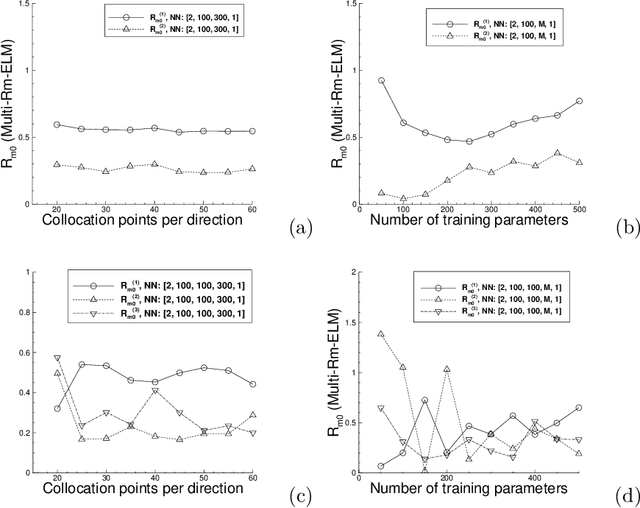
We consider the use of extreme learning machines (ELM) for computational partial differential equations (PDE). In ELM the hidden-layer coefficients in the neural network are assigned to random values generated on $[-R_m,R_m]$ and fixed, where $R_m$ is a user-provided constant, and the output-layer coefficients are trained by a linear or nonlinear least squares computation. We present a method for computing the optimal value of $R_m$ based on the differential evolution algorithm. The presented method enables us to illuminate the characteristics of the optimal $R_m$ for two types of ELM configurations: (i) Single-Rm-ELM, in which a single $R_m$ is used for generating the random coefficients in all the hidden layers, and (ii) Multi-Rm-ELM, in which multiple $R_m$ constants are involved with each used for generating the random coefficients of a different hidden layer. We adopt the optimal $R_m$ from this method and also incorporate other improvements into the ELM implementation. In particular, here we compute all the differential operators involving the output fields of the last hidden layer by a forward-mode auto-differentiation, as opposed to the reverse-mode auto-differentiation in a previous work. These improvements significantly reduce the network training time and enhance the ELM performance. We systematically compare the computational performance of the current improved ELM with that of the finite element method (FEM), both the classical second-order FEM and the high-order FEM with Lagrange elements of higher degrees, for solving a number of linear and nonlinear PDEs. It is shown that the current improved ELM far outperforms the classical FEM. Its computational performance is comparable to that of the high-order FEM for smaller problem sizes, and for larger problem sizes the ELM markedly outperforms the high-order FEM.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge