Jenn-Bing Ong
Protecting Big Data Privacy Using Randomized Tensor Network Decomposition and Dispersed Tensor Computation
Jan 04, 2021
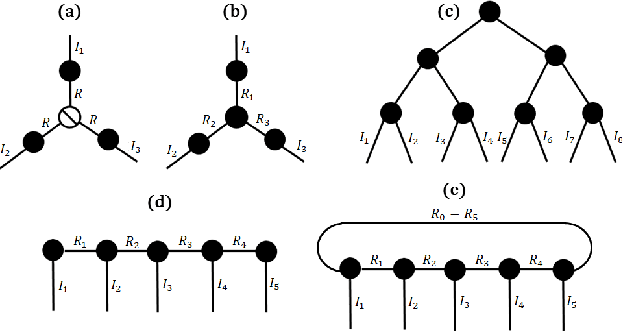
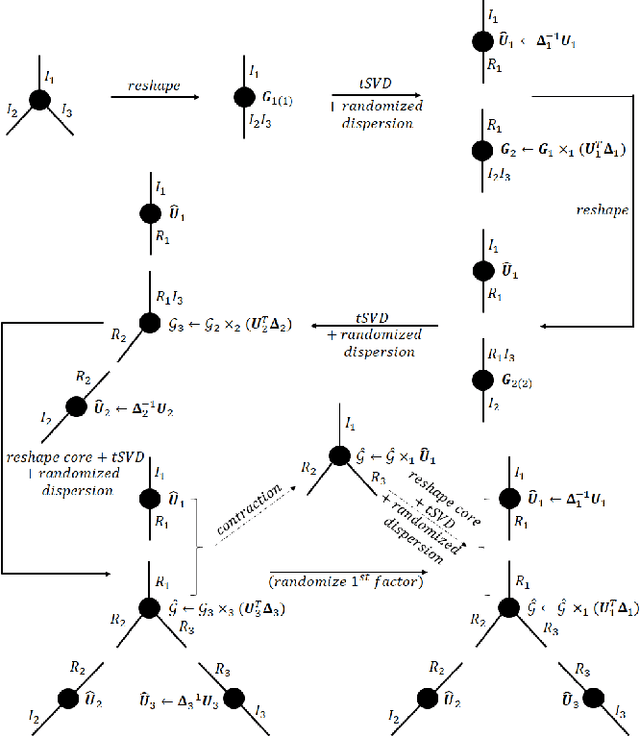
Abstract:Data privacy is an important issue for organizations and enterprises to securely outsource data storage, sharing, and computation on clouds / fogs. However, data encryption is complicated in terms of the key management and distribution; existing secure computation techniques are expensive in terms of computational / communication cost and therefore do not scale to big data computation. Tensor network decomposition and distributed tensor computation have been widely used in signal processing and machine learning for dimensionality reduction and large-scale optimization. However, the potential of distributed tensor networks for big data privacy preservation have not been considered before, this motivates the current study. Our primary intuition is that tensor network representations are mathematically non-unique, unlinkable, and uninterpretable; tensor network representations naturally support a range of multilinear operations for compressed and distributed / dispersed computation. Therefore, we propose randomized algorithms to decompose big data into randomized tensor network representations and analyze the privacy leakage for 1D to 3D data tensors. The randomness mainly comes from the complex structural information commonly found in big data; randomization is based on controlled perturbation applied to the tensor blocks prior to decomposition. The distributed tensor representations are dispersed on multiple clouds / fogs or servers / devices with metadata privacy, this provides both distributed trust and management to seamlessly secure big data storage, communication, sharing, and computation. Experiments show that the proposed randomization techniques are helpful for big data anonymization and efficient for big data storage and computation.
Convolutional Neural Networks with Transformed Input based on Robust Tensor Network Decomposition
Dec 11, 2018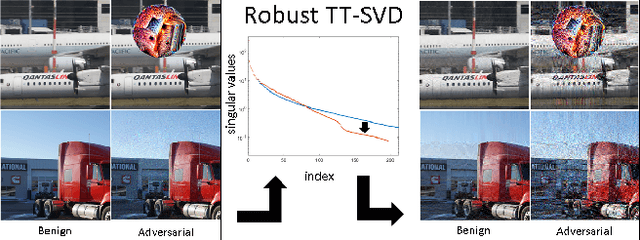
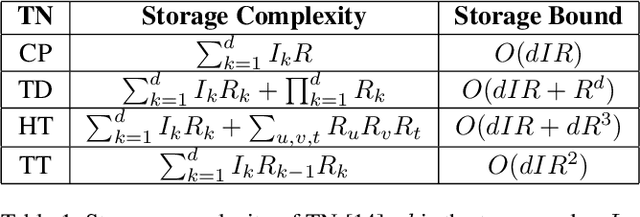
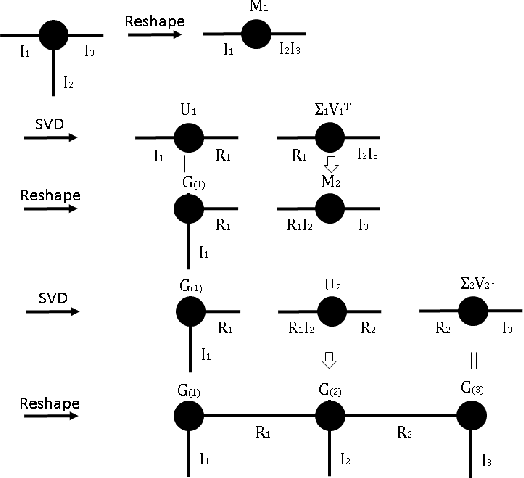
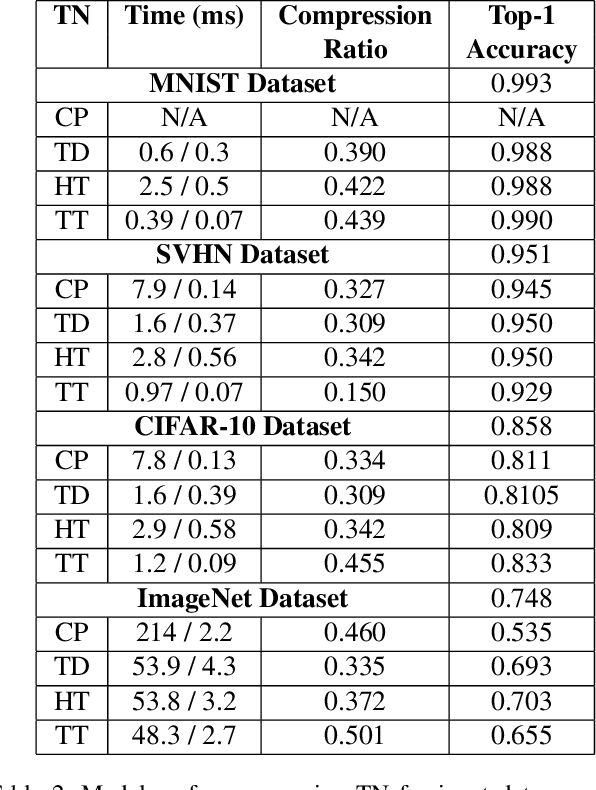
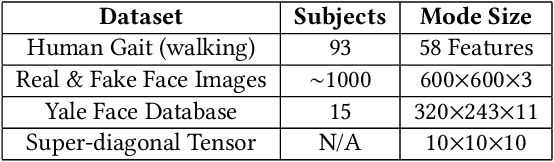
Abstract:Tensor network decomposition, originated from quantum physics to model entangled many-particle quantum systems, turns out to be a promising mathematical technique to efficiently represent and process big data in parsimonious manner. In this study, we show that tensor networks can systematically partition structured data, e.g. color images, for distributed storage and communication in privacy-preserving manner. Leveraging the sea of big data and metadata privacy, empirical results show that neighbouring subtensors with implicit information stored in tensor network formats cannot be identified for data reconstruction. This technique complements the existing encryption and randomization techniques which store explicit data representation at one place and highly susceptible to adversarial attacks such as side-channel attacks and de-anonymization. Furthermore, we propose a theory for adversarial examples that mislead convolutional neural networks to misclassification using subspace analysis based on singular value decomposition (SVD). The theory is extended to analyze higher-order tensors using tensor-train SVD (TT-SVD); it helps to explain the level of susceptibility of different datasets to adversarial attacks, the structural similarity of different adversarial attacks including global and localized attacks, and the efficacy of different adversarial defenses based on input transformation. An efficient and adaptive algorithm based on robust TT-SVD is then developed to detect strong and static adversarial attacks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge