Convolutional Neural Networks with Transformed Input based on Robust Tensor Network Decomposition
Paper and Code
Dec 11, 2018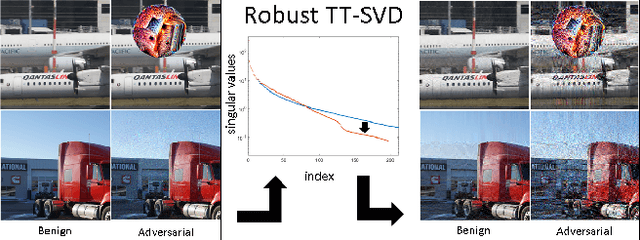
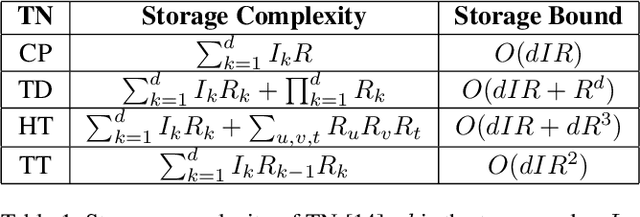
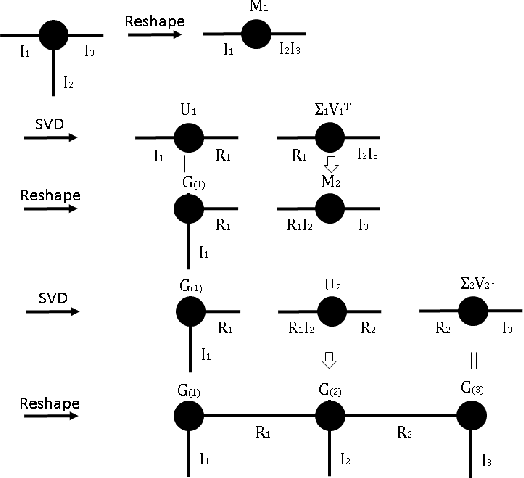
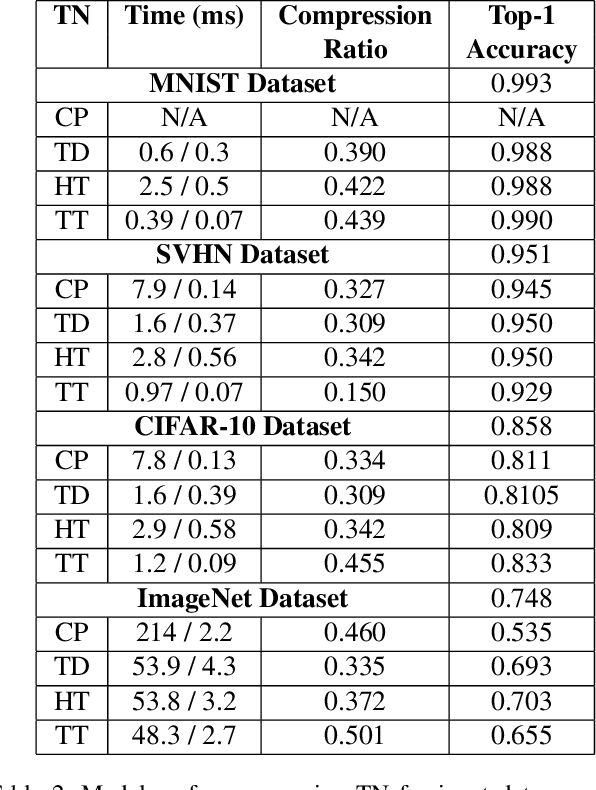
Tensor network decomposition, originated from quantum physics to model entangled many-particle quantum systems, turns out to be a promising mathematical technique to efficiently represent and process big data in parsimonious manner. In this study, we show that tensor networks can systematically partition structured data, e.g. color images, for distributed storage and communication in privacy-preserving manner. Leveraging the sea of big data and metadata privacy, empirical results show that neighbouring subtensors with implicit information stored in tensor network formats cannot be identified for data reconstruction. This technique complements the existing encryption and randomization techniques which store explicit data representation at one place and highly susceptible to adversarial attacks such as side-channel attacks and de-anonymization. Furthermore, we propose a theory for adversarial examples that mislead convolutional neural networks to misclassification using subspace analysis based on singular value decomposition (SVD). The theory is extended to analyze higher-order tensors using tensor-train SVD (TT-SVD); it helps to explain the level of susceptibility of different datasets to adversarial attacks, the structural similarity of different adversarial attacks including global and localized attacks, and the efficacy of different adversarial defenses based on input transformation. An efficient and adaptive algorithm based on robust TT-SVD is then developed to detect strong and static adversarial attacks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge