Parameter Identification for Electrochemical Models of Lithium-Ion Batteries Using Bayesian Optimization

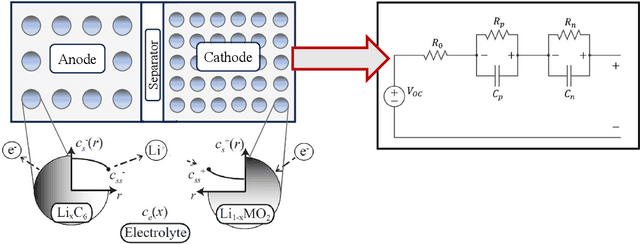
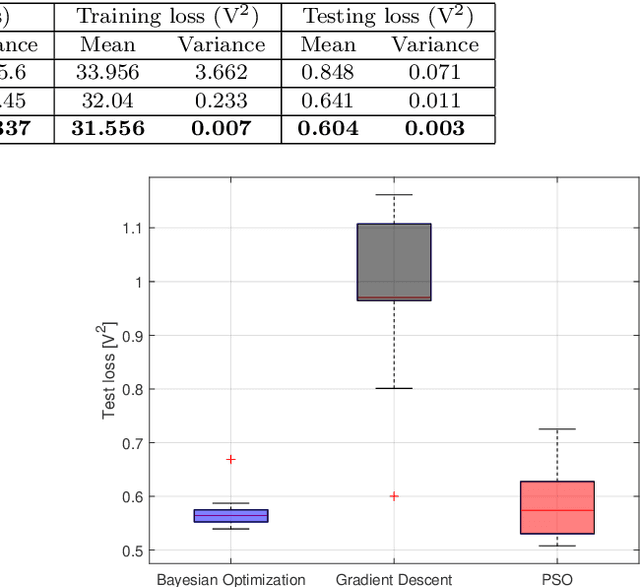
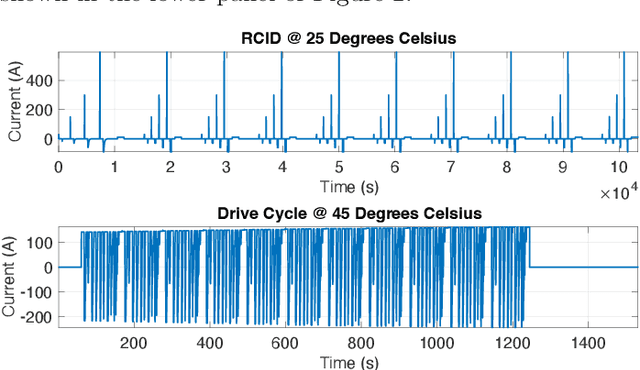
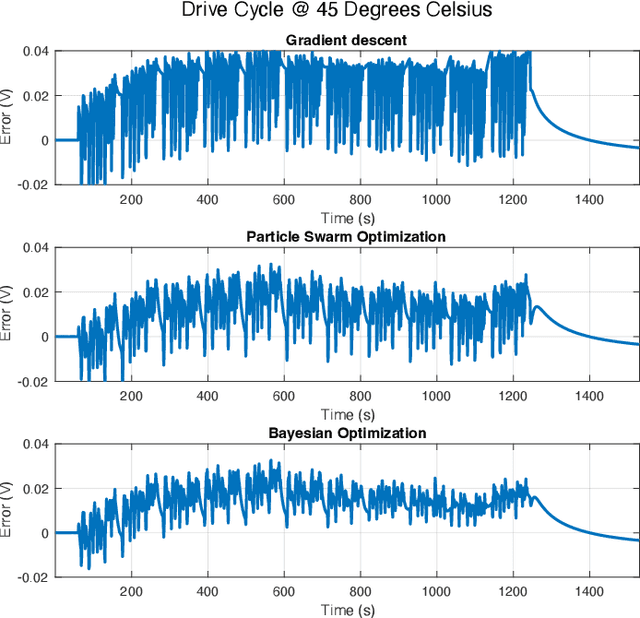
Efficient parameter identification of electrochemical models is crucial for accurate monitoring and control of lithium-ion cells. This process becomes challenging when applied to complex models that rely on a considerable number of interdependent parameters that affect the output response. Gradient-based and metaheuristic optimization techniques, although previously employed for this task, are limited by their lack of robustness, high computational costs, and susceptibility to local minima. In this study, Bayesian Optimization is used for tuning the dynamic parameters of an electrochemical equivalent circuit battery model (E-ECM) for a nickel-manganese-cobalt (NMC)-graphite cell. The performance of the Bayesian Optimization is compared with baseline methods based on gradient-based and metaheuristic approaches. The robustness of the parameter optimization method is tested by performing verification using an experimental drive cycle. The results indicate that Bayesian Optimization outperforms Gradient Descent and PSO optimization techniques, achieving reductions on average testing loss by 28.8% and 5.8%, respectively. Moreover, Bayesian optimization significantly reduces the variance in testing loss by 95.8% and 72.7%, respectively.

Neural collapse with unconstrained features

Neural collapse is an emergent phenomenon in deep learning that was recently discovered by Papyan, Han and Donoho. We propose a simple "unconstrained features model" in which neural collapse also emerges empirically. By studying this model, we provide some explanation for the emergence of neural collapse in terms of the landscape of empirical risk.

Some Limit Properties of Markov Chains Induced by Stochastic Recursive Algorithms

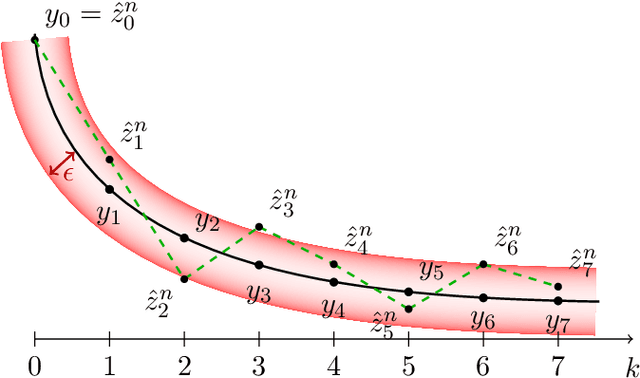
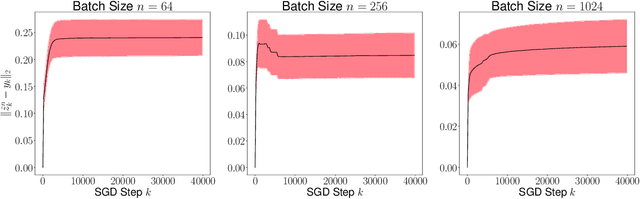
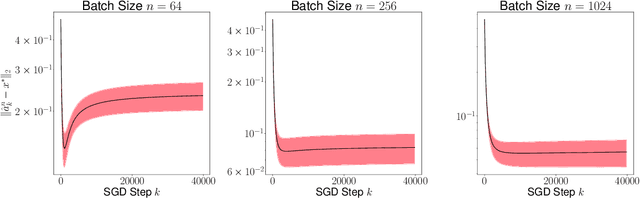
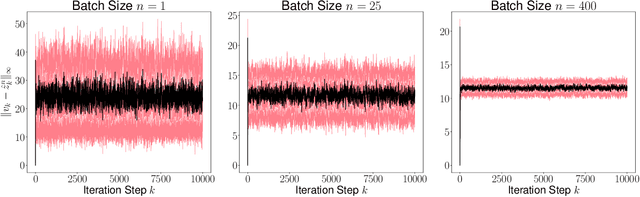
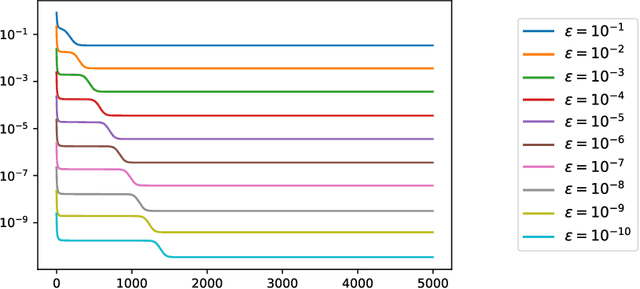
Recursive stochastic algorithms have gained significant attention in the recent past due to data driven applications. Examples include stochastic gradient descent for solving large-scale optimization problems and empirical dynamic programming algorithms for solving Markov decision problems. These recursive stochastic algorithms approximates certain contraction operators and can be viewed within the framework of iterated random maps. Accordingly, we consider iterated random maps over a Polish space that simulates a contraction operator over that Polish space. Assume that the iterated maps are indexed by $n$ such that as $n\rightarrow\infty$, each realization of the random map converges (in some sense) to the contraction map it is simulating. We show that starting from the same initial condition, the distribution of the random sequence generated by the iterated random maps converge weakly to the trajectory generated by the contraction operator. We further show that under certain conditions, the time average of the random sequence converge to the spatial mean of the invariant distribution. We then apply these results to logistic regression, empirical value iteration, empirical Q value iteration, and empirical relative value iteration for finite state finite action MDPs.