Some Limit Properties of Markov Chains Induced by Stochastic Recursive Algorithms

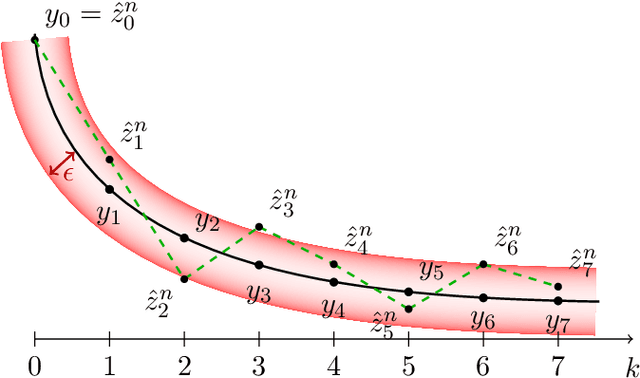
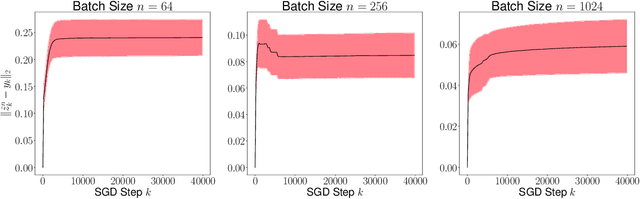
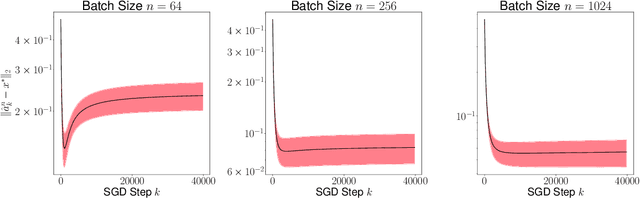
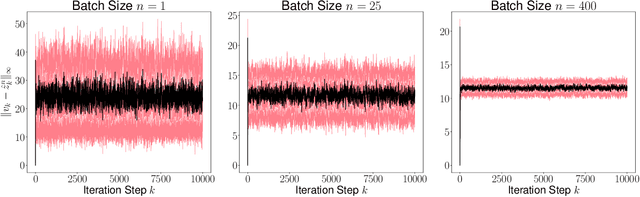
Recursive stochastic algorithms have gained significant attention in the recent past due to data driven applications. Examples include stochastic gradient descent for solving large-scale optimization problems and empirical dynamic programming algorithms for solving Markov decision problems. These recursive stochastic algorithms approximates certain contraction operators and can be viewed within the framework of iterated random maps. Accordingly, we consider iterated random maps over a Polish space that simulates a contraction operator over that Polish space. Assume that the iterated maps are indexed by $n$ such that as $n\rightarrow\infty$, each realization of the random map converges (in some sense) to the contraction map it is simulating. We show that starting from the same initial condition, the distribution of the random sequence generated by the iterated random maps converge weakly to the trajectory generated by the contraction operator. We further show that under certain conditions, the time average of the random sequence converge to the spatial mean of the invariant distribution. We then apply these results to logistic regression, empirical value iteration, empirical Q value iteration, and empirical relative value iteration for finite state finite action MDPs.