Distributed SGD Generalizes Well Under Asynchrony

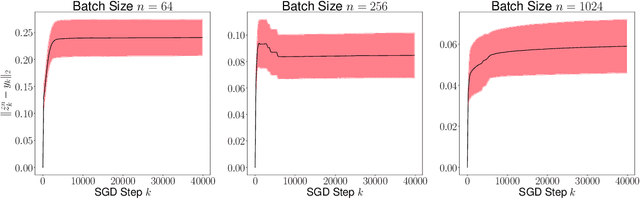
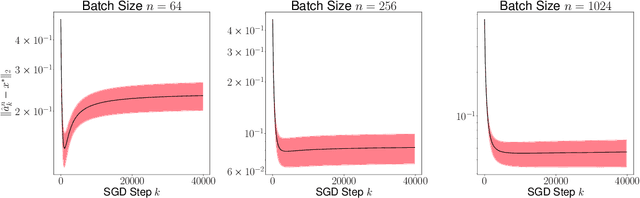
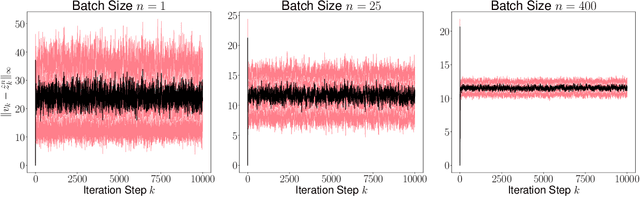
The performance of fully synchronized distributed systems has faced a bottleneck due to the big data trend, under which asynchronous distributed systems are becoming a major popularity due to their powerful scalability. In this paper, we study the generalization performance of stochastic gradient descent (SGD) on a distributed asynchronous system. The system consists of multiple worker machines that compute stochastic gradients which are further sent to and aggregated on a common parameter server to update the variables, and the communication in the system suffers from possible delays. Under the algorithm stability framework, we prove that distributed asynchronous SGD generalizes well given enough data samples in the training optimization. In particular, our results suggest to reduce the learning rate as we allow more asynchrony in the distributed system. Such adaptive learning rate strategy improves the stability of the distributed algorithm and reduces the corresponding generalization error. Then, we confirm our theoretical findings via numerical experiments.

Some Limit Properties of Markov Chains Induced by Stochastic Recursive Algorithms

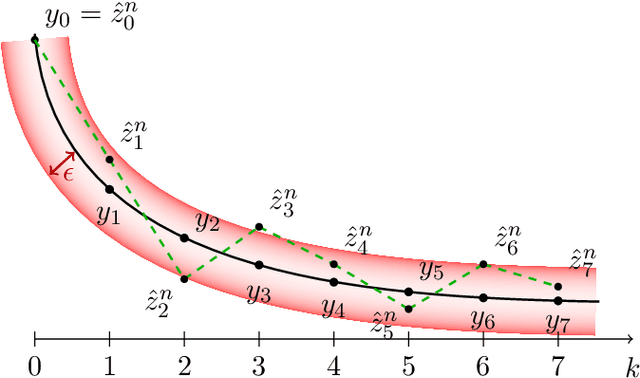
Recursive stochastic algorithms have gained significant attention in the recent past due to data driven applications. Examples include stochastic gradient descent for solving large-scale optimization problems and empirical dynamic programming algorithms for solving Markov decision problems. These recursive stochastic algorithms approximates certain contraction operators and can be viewed within the framework of iterated random maps. Accordingly, we consider iterated random maps over a Polish space that simulates a contraction operator over that Polish space. Assume that the iterated maps are indexed by $n$ such that as $n\rightarrow\infty$, each realization of the random map converges (in some sense) to the contraction map it is simulating. We show that starting from the same initial condition, the distribution of the random sequence generated by the iterated random maps converge weakly to the trajectory generated by the contraction operator. We further show that under certain conditions, the time average of the random sequence converge to the spatial mean of the invariant distribution. We then apply these results to logistic regression, empirical value iteration, empirical Q value iteration, and empirical relative value iteration for finite state finite action MDPs.