Jayanth Regatti
Befriending The Byzantines Through Reputation Scores
Jun 24, 2020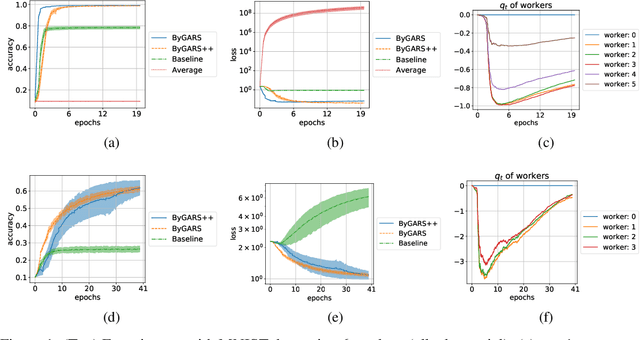
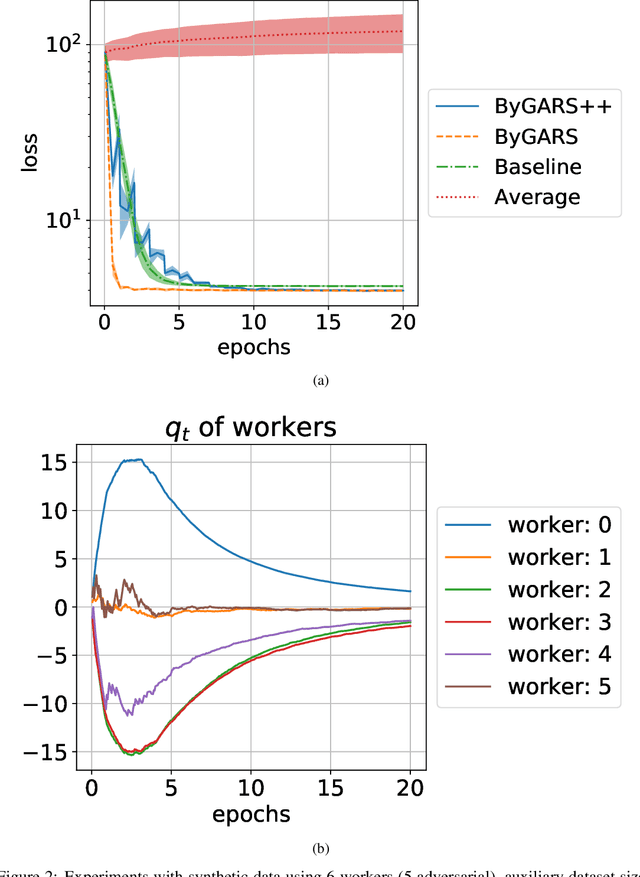
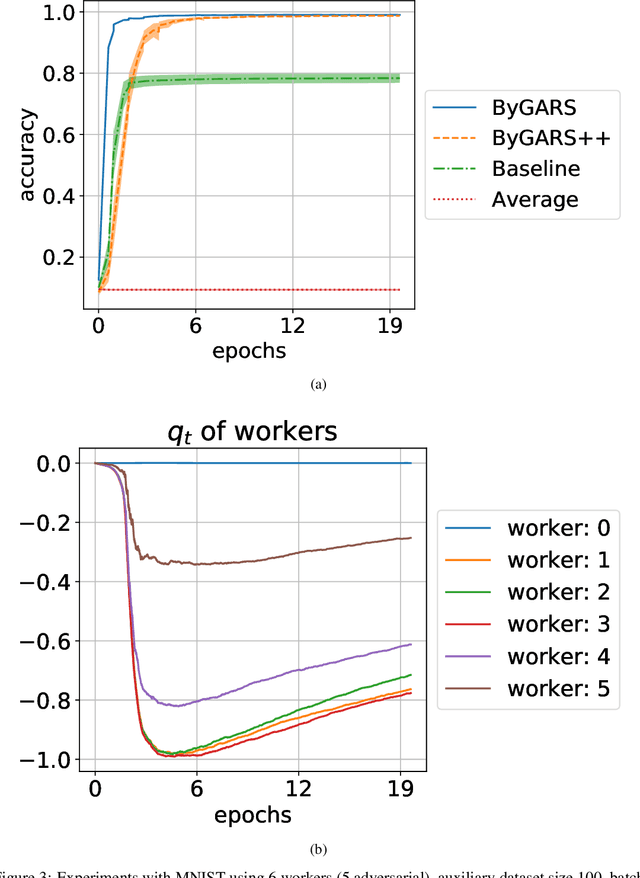
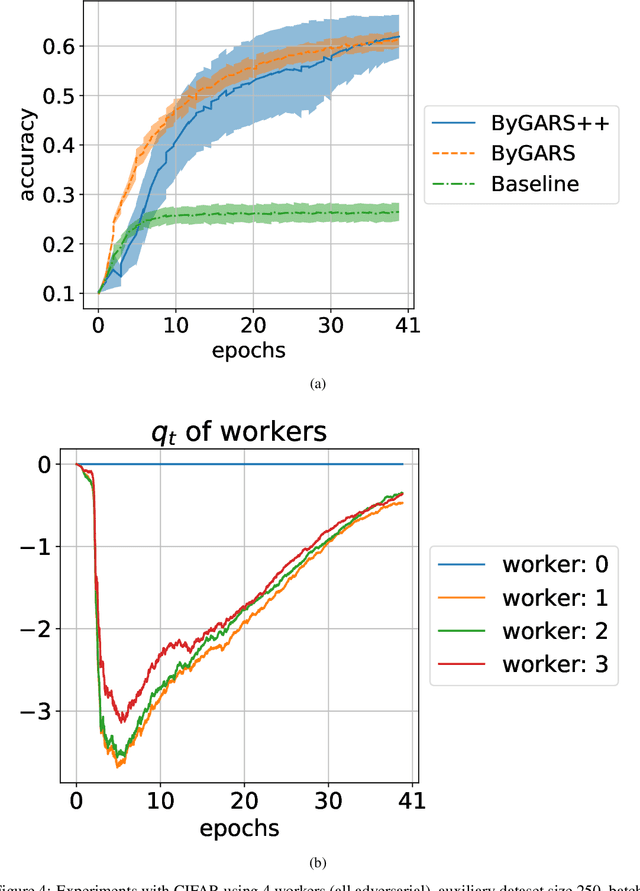
Abstract:We propose two novel stochastic gradient descent algorithms, ByGARS and ByGARS++, for distributed machine learning in the presence of Byzantine adversaries. In these algorithms, reputation score of workers are computed using an auxiliary dataset with a larger stepsize. This reputation score is then used for aggregating the gradients for stochastic gradient descent with a smaller stepsize. We show that using these reputation scores for gradient aggregation is robust to any number of Byzantine adversaries. In contrast to prior works targeting any number of adversaries, we improve the generalization performance by making use of some adversarial workers along with the benign ones. The computational complexity of ByGARS++ is the same as the usual stochastic gradient descent method with only an additional inner product computation. We establish its convergence for strongly convex loss functions and demonstrate the effectiveness of the algorithms for non-convex learning problems using MNIST and CIFAR-10 datasets.
Distributed SGD Generalizes Well Under Asynchrony
Sep 29, 2019



Abstract:The performance of fully synchronized distributed systems has faced a bottleneck due to the big data trend, under which asynchronous distributed systems are becoming a major popularity due to their powerful scalability. In this paper, we study the generalization performance of stochastic gradient descent (SGD) on a distributed asynchronous system. The system consists of multiple worker machines that compute stochastic gradients which are further sent to and aggregated on a common parameter server to update the variables, and the communication in the system suffers from possible delays. Under the algorithm stability framework, we prove that distributed asynchronous SGD generalizes well given enough data samples in the training optimization. In particular, our results suggest to reduce the learning rate as we allow more asynchrony in the distributed system. Such adaptive learning rate strategy improves the stability of the distributed algorithm and reduces the corresponding generalization error. Then, we confirm our theoretical findings via numerical experiments.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge