Befriending The Byzantines Through Reputation Scores

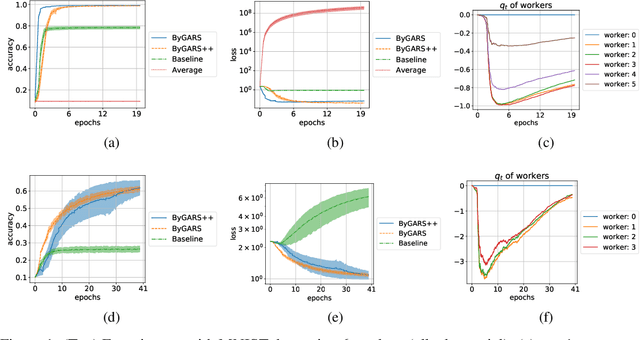
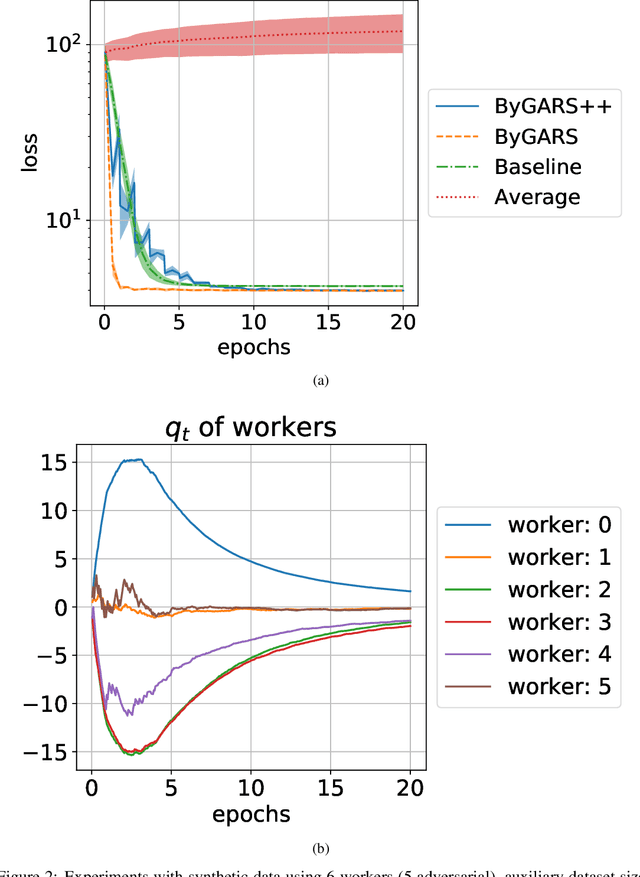
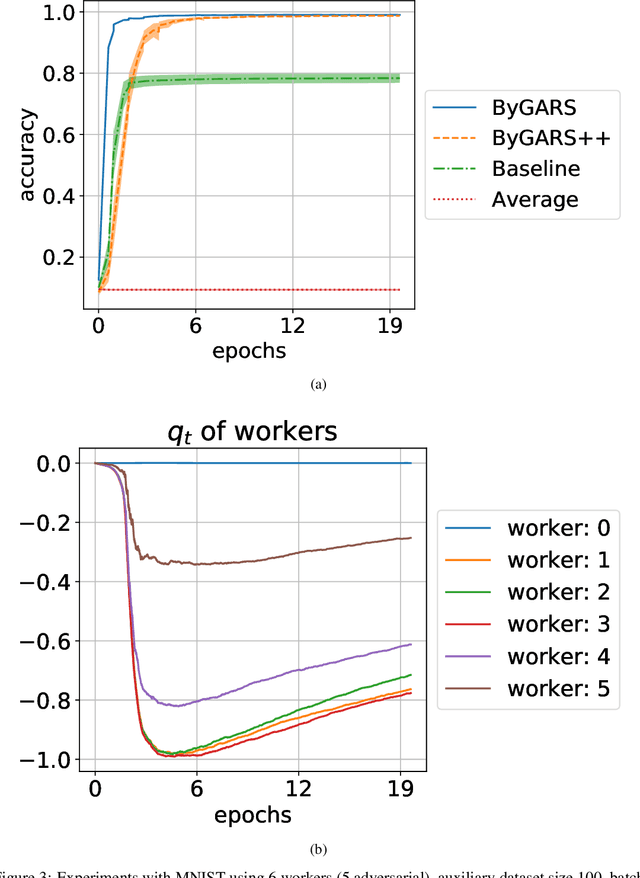
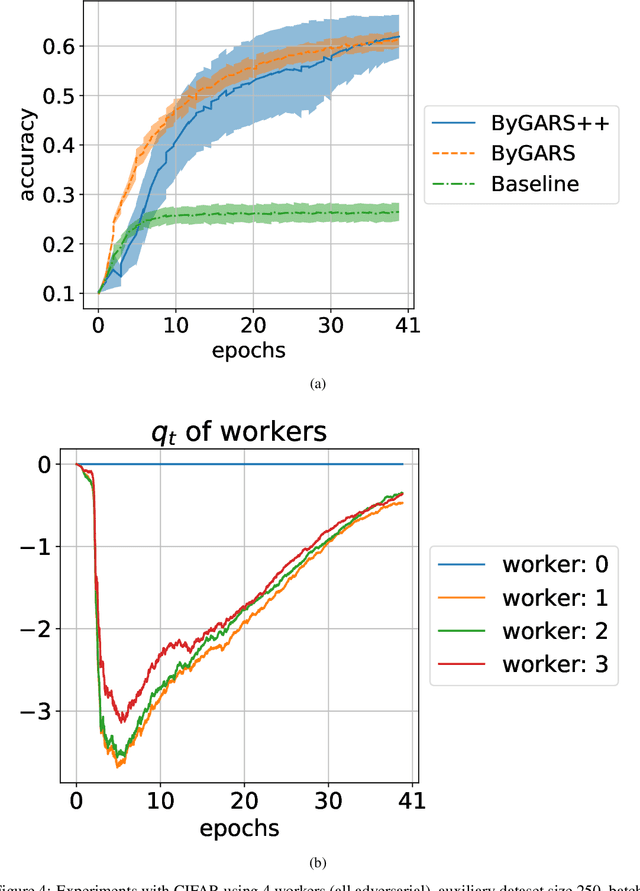
We propose two novel stochastic gradient descent algorithms, ByGARS and ByGARS++, for distributed machine learning in the presence of Byzantine adversaries. In these algorithms, reputation score of workers are computed using an auxiliary dataset with a larger stepsize. This reputation score is then used for aggregating the gradients for stochastic gradient descent with a smaller stepsize. We show that using these reputation scores for gradient aggregation is robust to any number of Byzantine adversaries. In contrast to prior works targeting any number of adversaries, we improve the generalization performance by making use of some adversarial workers along with the benign ones. The computational complexity of ByGARS++ is the same as the usual stochastic gradient descent method with only an additional inner product computation. We establish its convergence for strongly convex loss functions and demonstrate the effectiveness of the algorithms for non-convex learning problems using MNIST and CIFAR-10 datasets.