Sketch-and-solve approaches to k-means clustering by semidefinite programming

We introduce a sketch-and-solve approach to speed up the Peng-Wei semidefinite relaxation of k-means clustering. When the data is appropriately separated we identify the k-means optimal clustering. Otherwise, our approach provides a high-confidence lower bound on the optimal k-means value. This lower bound is data-driven; it does not make any assumption on the data nor how it is generated. We provide code and an extensive set of numerical experiments where we use this approach to certify approximate optimality of clustering solutions obtained by k-means++.

Group-invariant max filtering

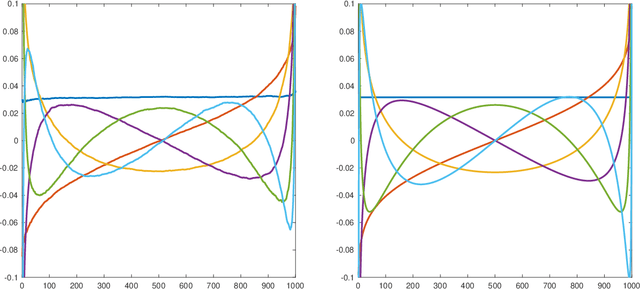
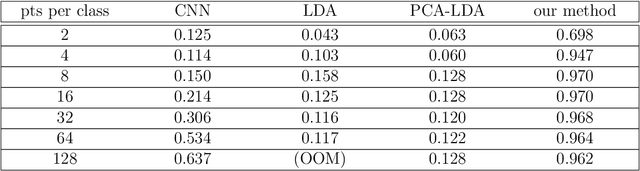
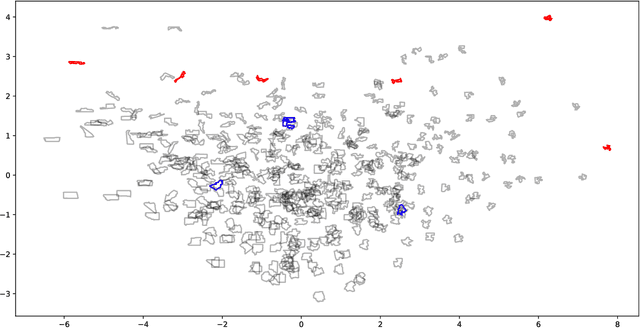
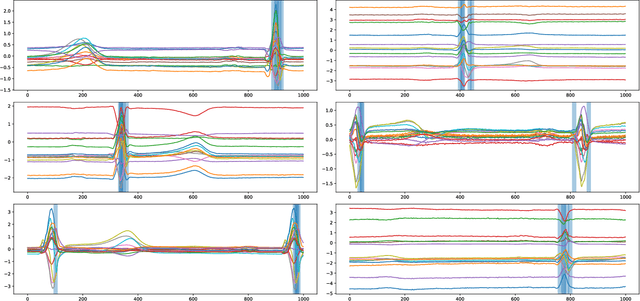
Given a real inner product space $V$ and a group $G$ of linear isometries, we construct a family of $G$-invariant real-valued functions on $V$ that we call max filters. In the case where $V=\mathbb{R}^d$ and $G$ is finite, a suitable max filter bank separates orbits, and is even bilipschitz in the quotient metric. In the case where $V=L^2(\mathbb{R}^d)$ and $G$ is the group of translation operators, a max filter exhibits stability to diffeomorphic distortion like that of the scattering transform introduced by Mallat. We establish that max filters are well suited for various classification tasks, both in theory and in practice.

Neural collapse with unconstrained features

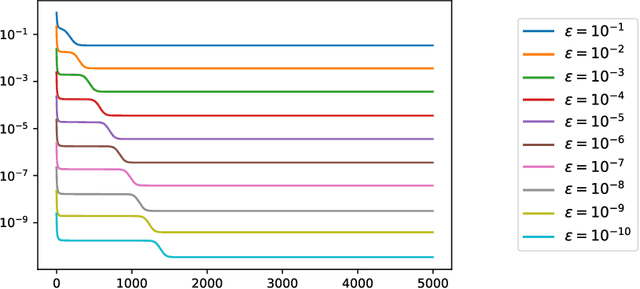
Neural collapse is an emergent phenomenon in deep learning that was recently discovered by Papyan, Han and Donoho. We propose a simple "unconstrained features model" in which neural collapse also emerges empirically. By studying this model, we provide some explanation for the emergence of neural collapse in terms of the landscape of empirical risk.

Lie PCA: Density estimation for symmetric manifolds

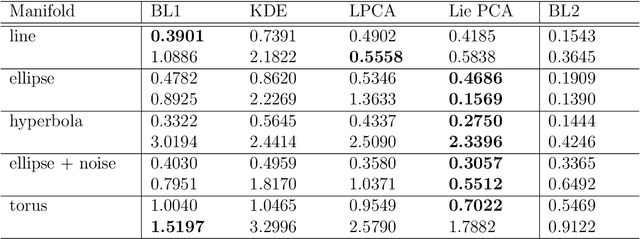
We introduce an extension to local principal component analysis for learning symmetric manifolds. In particular, we use a spectral method to approximate the Lie algebra corresponding to the symmetry group of the underlying manifold. We derive the sample complexity of our method for a variety of manifolds before applying it to various data sets for improved density estimation.

Sketching semidefinite programs for faster clustering

Many clustering problems enjoy solutions by semidefinite programming. Theoretical results in this vein frequently consider data with a planted clustering and a notion of signal strength such that the semidefinite program exactly recovers the planted clustering when the signal strength is sufficiently large. In practice, semidefinite programs are notoriously slow, and so speedups are welcome. In this paper, we show how to sketch a popular semidefinite relaxation of a graph clustering problem known as minimum bisection, and our analysis supports a meta-claim that the clustering task is less computationally burdensome when there is more signal.

SqueezeFit: Label-aware dimensionality reduction by semidefinite programming

Given labeled points in a high-dimensional vector space, we seek a low-dimensional subspace such that projecting onto this subspace maintains some prescribed distance between points of differing labels. Intended applications include compressive classification. Taking inspiration from large margin nearest neighbor classification, this paper introduces a semidefinite relaxation of this problem. Unlike its predecessors, this relaxation is amenable to theoretical analysis, allowing us to provably recover a planted projection operator from the data.

SUNLayer: Stable denoising with generative networks

It has been experimentally established that deep neural networks can be used to produce good generative models for real world data. It has also been established that such generative models can be exploited to solve classical inverse problems like compressed sensing and super resolution. In this work we focus on the classical signal processing problem of image denoising. We propose a theoretical setting that uses spherical harmonics to identify what mathematical properties of the activation functions will allow signal denoising with local methods.

Monte Carlo approximation certificates for k-means clustering

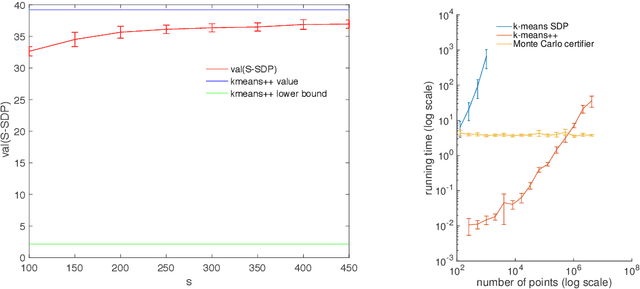
Efficient algorithms for $k$-means clustering frequently converge to suboptimal partitions, and given a partition, it is difficult to detect $k$-means optimality. In this paper, we develop an a posteriori certifier of approximate optimality for $k$-means clustering. The certifier is a sub-linear Monte Carlo algorithm based on Peng and Wei's semidefinite relaxation of $k$-means. In particular, solving the relaxation for small random samples of the dataset produces a high-confidence lower bound on the $k$-means objective, and being sub-linear, our algorithm is faster than $k$-means++ when the number of data points is large. We illustrate the performance of our algorithm with both numerical experiments and a performance guarantee: If the data points are drawn independently from any mixture of two Gaussians over $\mathbb{R}^m$ with identity covariance, then with probability $1-O(1/m)$, our $\operatorname{poly}(m)$-time algorithm produces a 3-approximation certificate with 99% confidence.

Clustering subgaussian mixtures by semidefinite programming

We introduce a model-free relax-and-round algorithm for k-means clustering based on a semidefinite relaxation due to Peng and Wei. The algorithm interprets the SDP output as a denoised version of the original data and then rounds this output to a hard clustering. We provide a generic method for proving performance guarantees for this algorithm, and we analyze the algorithm in the context of subgaussian mixture models. We also study the fundamental limits of estimating Gaussian centers by k-means clustering in order to compare our approximation guarantee to the theoretically optimal k-means clustering solution.

Probably certifiably correct k-means clustering

Recently, Bandeira [arXiv:1509.00824] introduced a new type of algorithm (the so-called probably certifiably correct algorithm) that combines fast solvers with the optimality certificates provided by convex relaxations. In this paper, we devise such an algorithm for the problem of k-means clustering. First, we prove that Peng and Wei's semidefinite relaxation of k-means is tight with high probability under a distribution of planted clusters called the stochastic ball model. Our proof follows from a new dual certificate for integral solutions of this semidefinite program. Next, we show how to test the optimality of a proposed k-means solution using this dual certificate in quasilinear time. Finally, we analyze a version of spectral clustering from Peng and Wei that is designed to solve k-means in the case of two clusters. In particular, we show that this quasilinear-time method typically recovers planted clusters under the stochastic ball model.