Monte Carlo approximation certificates for k-means clustering
Paper and Code
Oct 03, 2017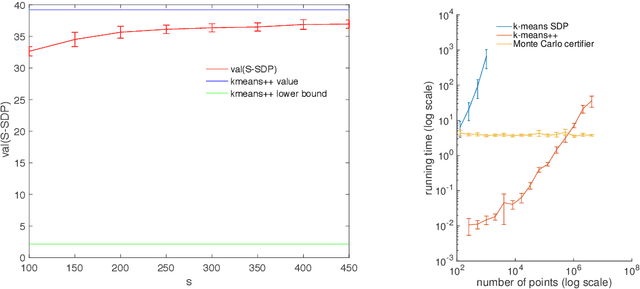
Efficient algorithms for $k$-means clustering frequently converge to suboptimal partitions, and given a partition, it is difficult to detect $k$-means optimality. In this paper, we develop an a posteriori certifier of approximate optimality for $k$-means clustering. The certifier is a sub-linear Monte Carlo algorithm based on Peng and Wei's semidefinite relaxation of $k$-means. In particular, solving the relaxation for small random samples of the dataset produces a high-confidence lower bound on the $k$-means objective, and being sub-linear, our algorithm is faster than $k$-means++ when the number of data points is large. We illustrate the performance of our algorithm with both numerical experiments and a performance guarantee: If the data points are drawn independently from any mixture of two Gaussians over $\mathbb{R}^m$ with identity covariance, then with probability $1-O(1/m)$, our $\operatorname{poly}(m)$-time algorithm produces a 3-approximation certificate with 99% confidence.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge