Tailoring Generative Adversarial Networks for Smooth Airfoil Design

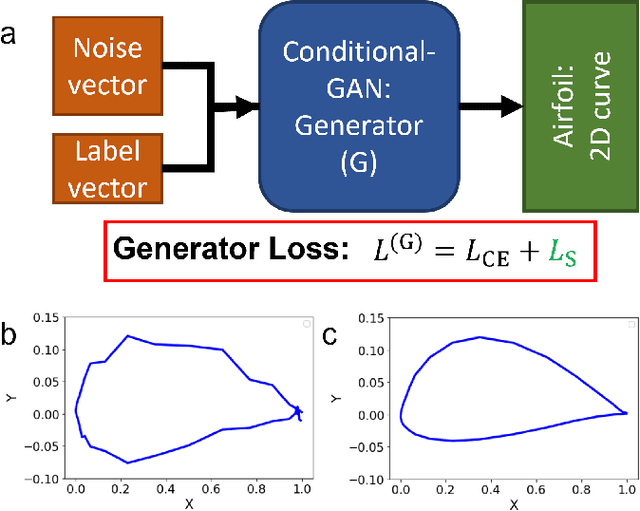
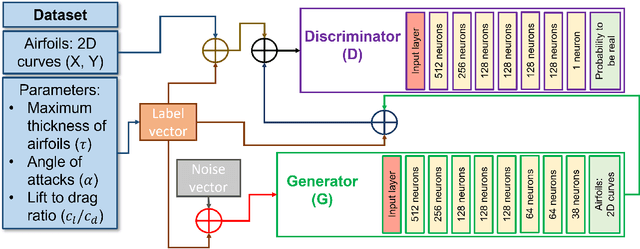
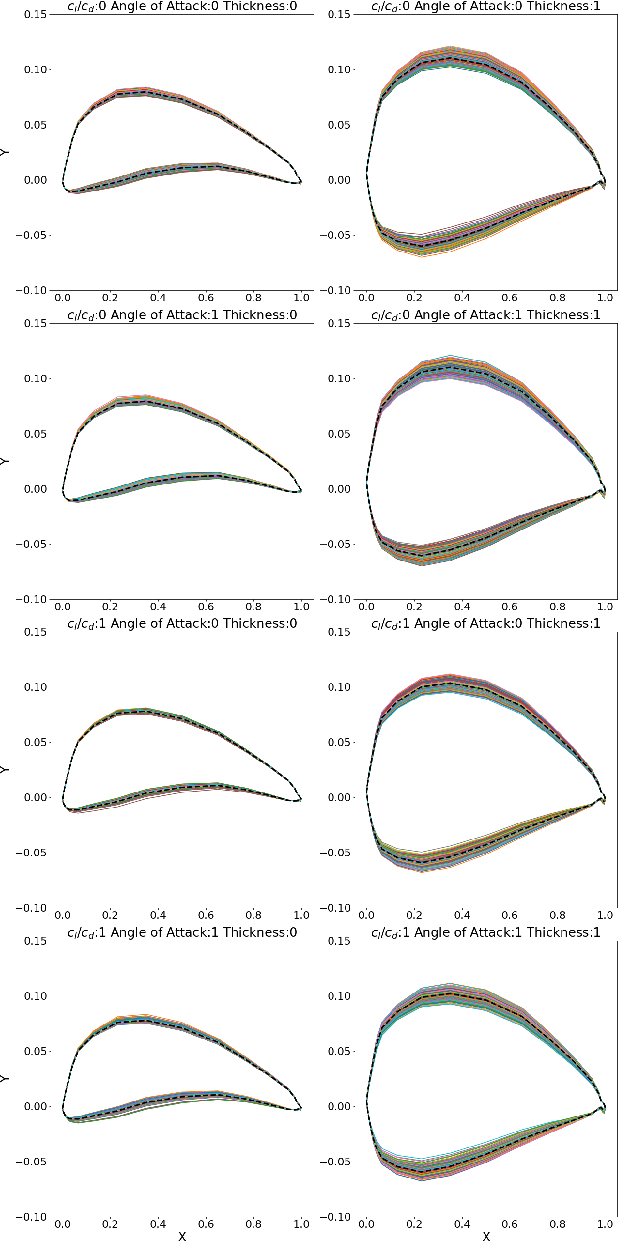
In the realm of aerospace design, achieving smooth curves is paramount, particularly when crafting objects such as airfoils. Generative Adversarial Network (GAN), a widely employed generative AI technique, has proven instrumental in synthesizing airfoil designs. However, a common limitation of GAN is the inherent lack of smoothness in the generated airfoil surfaces. To address this issue, we present a GAN model featuring a customized loss function built to produce seamlessly contoured airfoil designs. Additionally, our model demonstrates a substantial increase in design diversity compared to a conventional GAN augmented with a post-processing smoothing filter.

Generalizable Neural Physics Solvers by Baldwinian Evolution

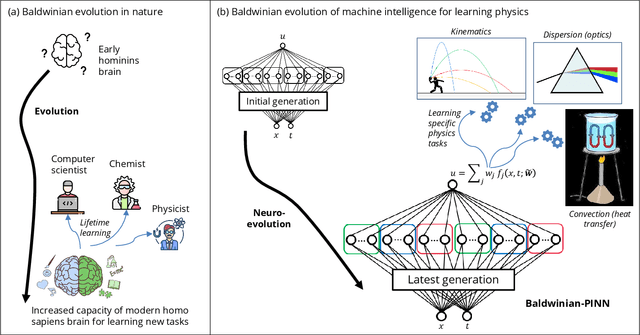
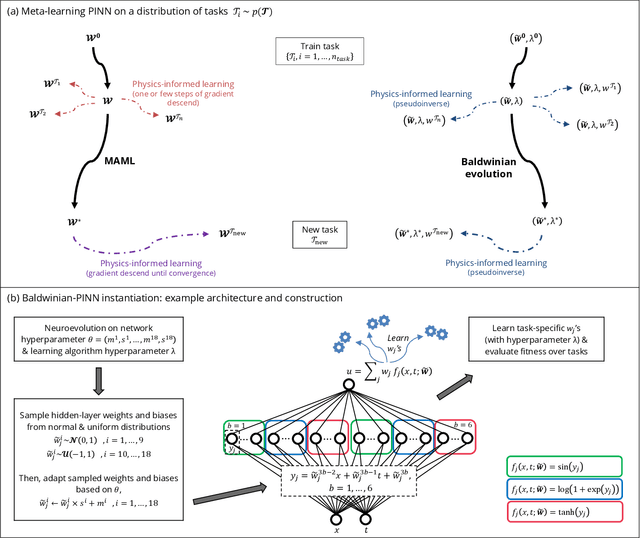
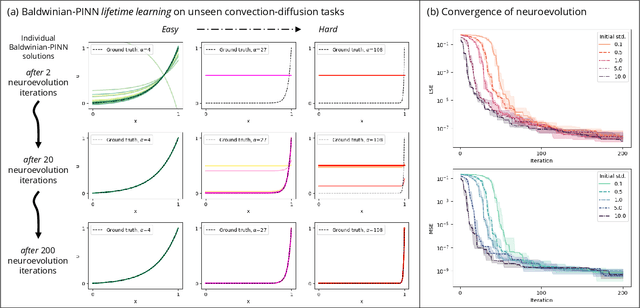
Physics-informed neural networks (PINNs) are at the forefront of scientific machine learning, making possible the creation of machine intelligence that is cognizant of physical laws and able to accurately simulate them. In this paper, the potential of discovering PINNs that generalize over an entire family of physics tasks is studied, for the first time, through a biological lens of the Baldwin effect. Drawing inspiration from the neurodevelopment of precocial species that have evolved to learn, predict and react quickly to their environment, we envision PINNs that are pre-wired with connection strengths inducing strong biases towards efficient learning of physics. To this end, evolutionary selection pressure (guided by proficiency over a family of tasks) is coupled with lifetime learning (to specialize on a smaller subset of those tasks) to produce PINNs that demonstrate fast and physics-compliant prediction capabilities across a range of empirically challenging problem instances. The Baldwinian approach achieves an order of magnitude improvement in prediction accuracy at a fraction of the computation cost compared to state-of-the-art results with PINNs meta-learned by gradient descent. This paper marks a leap forward in the meta-learning of PINNs as generalizable physics solvers.

LSA-PINN: Linear Boundary Connectivity Loss for Solving PDEs on Complex Geometry

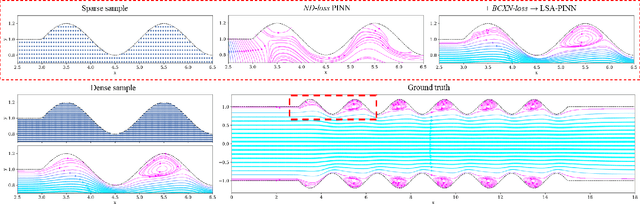
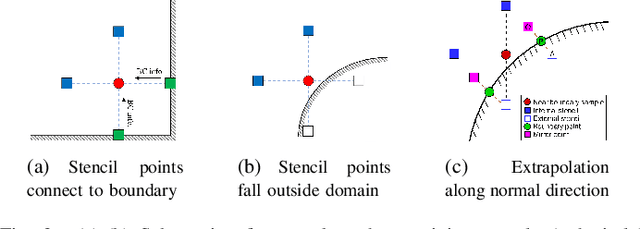
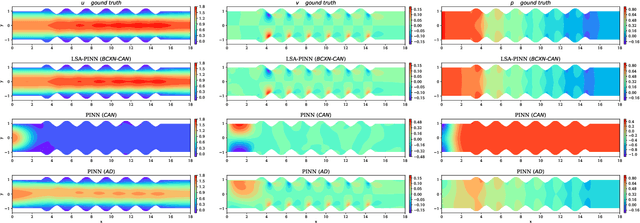
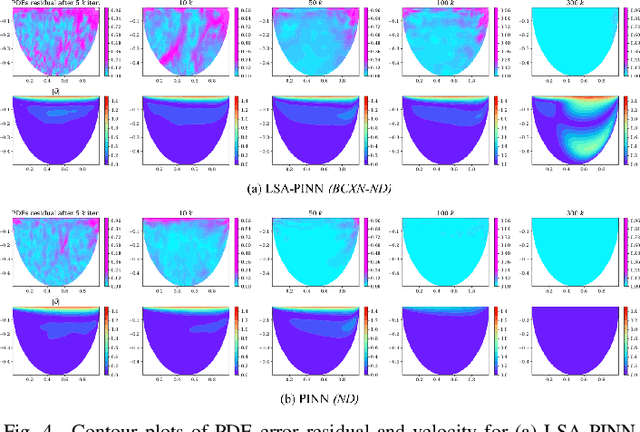
We present a novel loss formulation for efficient learning of complex dynamics from governing physics, typically described by partial differential equations (PDEs), using physics-informed neural networks (PINNs). In our experiments, existing versions of PINNs are seen to learn poorly in many problems, especially for complex geometries, as it becomes increasingly difficult to establish appropriate sampling strategy at the near boundary region. Overly dense sampling can adversely impede training convergence if the local gradient behaviors are too complex to be adequately modelled by PINNs. On the other hand, if the samples are too sparse, existing PINNs tend to overfit the near boundary region, leading to incorrect solution. To prevent such issues, we propose a new Boundary Connectivity (BCXN) loss function which provides linear local structure approximation (LSA) to the gradient behaviors at the boundary for PINN. Our BCXN-loss implicitly imposes local structure during training, thus facilitating fast physics-informed learning across entire problem domains with order of magnitude sparser training samples. This LSA-PINN method shows a few orders of magnitude smaller errors than existing methods in terms of the standard L2-norm metric, while using dramatically fewer training samples and iterations. Our proposed LSA-PINN does not pose any requirement on the differentiable property of the networks, and we demonstrate its benefits and ease of implementation on both multi-layer perceptron and convolutional neural network versions as commonly used in current PINN literature.

Graph Neural Network Based Surrogate Model of Physics Simulations for Geometry Design

Computational Intelligence (CI) techniques have shown great potential as a surrogate model of expensive physics simulation, with demonstrated ability to make fast predictions, albeit at the expense of accuracy in some cases. For many scientific and engineering problems involving geometrical design, it is desirable for the surrogate models to precisely describe the change in geometry and predict the consequences. In that context, we develop graph neural networks (GNNs) as fast surrogate models for physics simulation, which allow us to directly train the models on 2/3D geometry designs that are represented by an unstructured mesh or point cloud, without the need for any explicit or hand-crafted parameterization. We utilize an encoder-processor-decoder-type architecture which can flexibly make prediction at both node level and graph level. The performance of our proposed GNN-based surrogate model is demonstrated on 2 example applications: feature designs in the domain of additive engineering and airfoil design in the domain of aerodynamics. The models show good accuracy in their predictions on a separate set of test geometries after training, with almost instant prediction speeds, as compared to O(hour) for the high-fidelity simulations required otherwise.

JAX-Accelerated Neuroevolution of Physics-informed Neural Networks: Benchmarks and Experimental Results

This paper introduces the use of evolutionary algorithms for solving differential equations. The solution is obtained by optimizing a deep neural network whose loss function is defined by the residual terms from the differential equations. Recent studies have used stochastic gradient descent (SGD) variants to train these physics-informed neural networks (PINNs), but these methods can struggle to find accurate solutions due to optimization challenges. When solving differential equations, it is important to find the globally optimum parameters of the network, rather than just finding a solution that works well during training. SGD only searches along a single gradient direction, so it may not be the best approach for training PINNs with their accompanying complex optimization landscapes. In contrast, evolutionary algorithms perform a parallel exploration of different solutions in order to avoid getting stuck in local optima and can potentially find more accurate solutions. However, evolutionary algorithms can be slow, which can make them difficult to use in practice. To address this, we provide a set of five benchmark problems with associated performance metrics and baseline results to support the development of evolutionary algorithms for enhanced PINN training. As a baseline, we evaluate the performance and speed of using the widely adopted Covariance Matrix Adaptation Evolution Strategy (CMA-ES) for solving PINNs. We provide the loss and training time for CMA-ES run on TensorFlow, and CMA-ES and SGD run on JAX (with GPU acceleration) for the five benchmark problems. Our results show that JAX-accelerated evolutionary algorithms, particularly CMA-ES, can be a useful approach for solving differential equations. We hope that our work will support the exploration and development of alternative optimization algorithms for the complex task of optimizing PINNs.

Design of Turing Systems with Physics-Informed Neural Networks

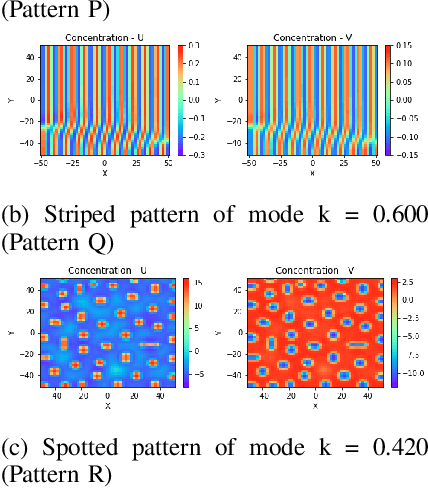
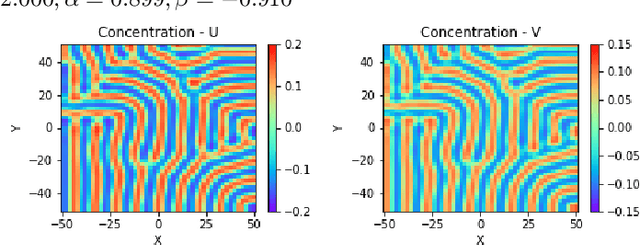
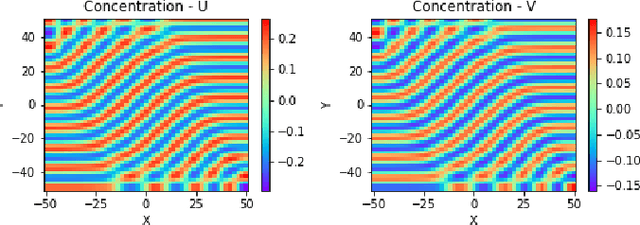
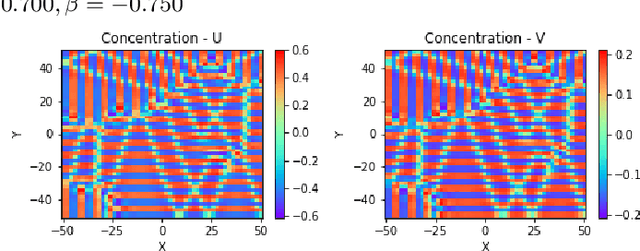
Reaction-diffusion (Turing) systems are fundamental to the formation of spatial patterns in nature and engineering. These systems are governed by a set of non-linear partial differential equations containing parameters that determine the rate of constituent diffusion and reaction. Critically, these parameters, such as diffusion coefficient, heavily influence the mode and type of the final pattern, and quantitative characterization and knowledge of these parameters can aid in bio-mimetic design or understanding of real-world systems. However, the use of numerical methods to infer these parameters can be difficult and computationally expensive. Typically, adjoint solvers may be used, but they are frequently unstable for very non-linear systems. Alternatively, massive amounts of iterative forward simulations are used to find the best match, but this is extremely effortful. Recently, physics-informed neural networks have been proposed as a means for data-driven discovery of partial differential equations, and have seen success in various applications. Thus, we investigate the use of physics-informed neural networks as a tool to infer key parameters in reaction-diffusion systems in the steady-state for scientific discovery or design. Our proof-of-concept results show that the method is able to infer parameters for different pattern modes and types with errors of less than 10\%. In addition, the stochastic nature of this method can be exploited to provide multiple parameter alternatives to the desired pattern, highlighting the versatility of this method for bio-mimetic design. This work thus demonstrates the utility of physics-informed neural networks for inverse parameter inference of reaction-diffusion systems to enhance scientific discovery and design.

FastFlow: AI for Fast Urban Wind Velocity Prediction

Data-driven approaches, including deep learning, have shown great promise as surrogate models across many domains. These extend to various areas in sustainability. An interesting direction for which data-driven methods have not been applied much yet is in the quick quantitative evaluation of urban layouts for planning and design. In particular, urban designs typically involve complex trade-offs between multiple objectives, including limits on urban build-up and/or consideration of urban heat island effect. Hence, it can be beneficial to urban planners to have a fast surrogate model to predict urban characteristics of a hypothetical layout, e.g. pedestrian-level wind velocity, without having to run computationally expensive and time-consuming high-fidelity numerical simulations. This fast surrogate can then be potentially integrated into other design optimization frameworks, including generative models or other gradient-based methods. Here we present the use of CNNs for urban layout characterization that is typically done via high-fidelity numerical simulation. We further apply this model towards a first demonstration of its utility for data-driven pedestrian-level wind velocity prediction. The data set in this work comprises results from high-fidelity numerical simulations of wind velocities for a diverse set of realistic urban layouts, based on randomized samples from a real-world, highly built-up urban city. We then provide prediction results obtained from the trained CNN, demonstrating test errors of under 0.1 m/s for previously unseen urban layouts. We further illustrate how this can be useful for purposes such as rapid evaluation of pedestrian wind velocity for a potential new layout. It is hoped that this data set will further accelerate research in data-driven urban AI, even as our baseline model facilitates quantitative comparison to future methods.

Robustness of Physics-Informed Neural Networks to Noise in Sensor Data

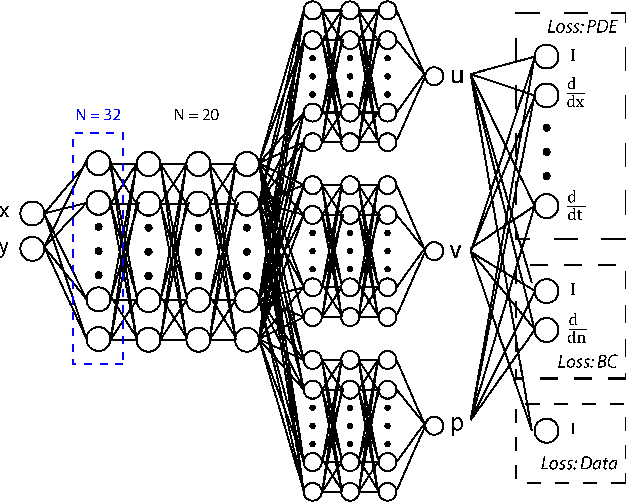
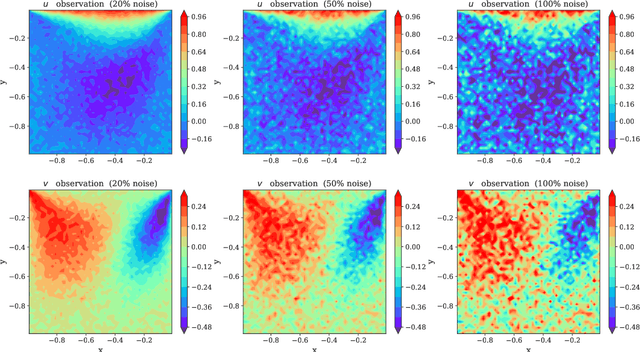
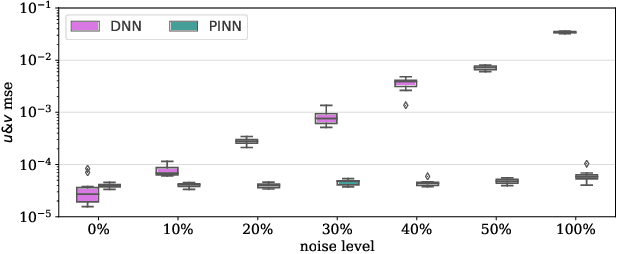
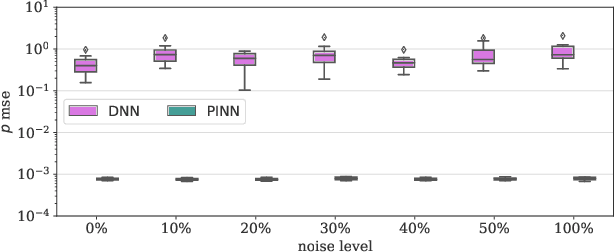
Physics-Informed Neural Networks (PINNs) have been shown to be an effective way of incorporating physics-based domain knowledge into neural network models for many important real-world systems. They have been particularly effective as a means of inferring system information based on data, even in cases where data is scarce. Most of the current work however assumes the availability of high-quality data. In this work, we further conduct a preliminary investigation of the robustness of physics-informed neural networks to the magnitude of noise in the data. Interestingly, our experiments reveal that the inclusion of physics in the neural network is sufficient to negate the impact of noise in data originating from hypothetical low quality sensors with high signal-to-noise ratios of up to 1. The resultant predictions for this test case are seen to still match the predictive value obtained for equivalent data obtained from high-quality sensors with potentially 10x less noise. This further implies the utility of physics-informed neural network modeling for making sense of data from sensor networks in the future, especially with the advent of Industry 4.0 and the increasing trend towards ubiquitous deployment of low-cost sensors which are typically noisier.

CAN-PINN: A Fast Physics-Informed Neural Network Based on Coupled-Automatic-Numerical Differentiation Method

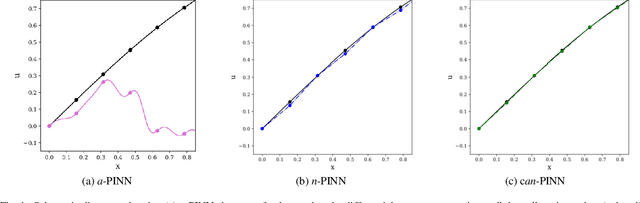
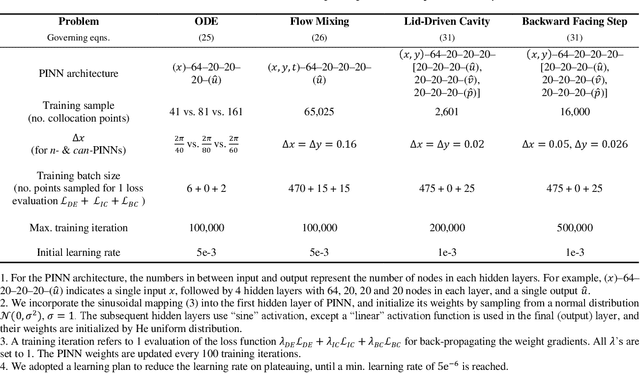
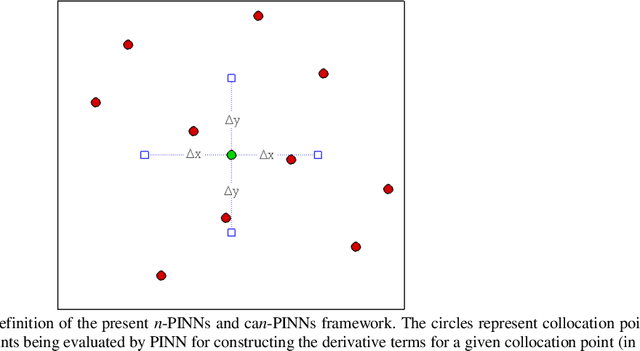
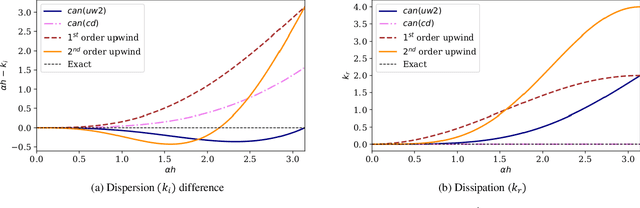
In this study, novel physics-informed neural network (PINN) methods for coupling neighboring support points and automatic differentiation (AD) through Taylor series expansion are proposed to allow efficient training with improved accuracy. The computation of differential operators required for PINNs loss evaluation at collocation points are conventionally obtained via AD. Although AD has the advantage of being able to compute the exact gradients at any point, such PINNs can only achieve high accuracies with large numbers of collocation points, otherwise they are prone to optimizing towards unphysical solution. To make PINN training fast, the dual ideas of using numerical differentiation (ND)-inspired method and coupling it with AD are employed to define the loss function. The ND-based formulation for training loss can strongly link neighboring collocation points to enable efficient training in sparse sample regimes, but its accuracy is restricted by the interpolation scheme. The proposed coupled-automatic-numerical differentiation framework, labeled as can-PINN, unifies the advantages of AD and ND, providing more robust and efficient training than AD-based PINNs, while further improving accuracy by up to 1-2 orders of magnitude relative to ND-based PINNs. For a proof-of-concept demonstration of this can-scheme to fluid dynamic problems, two numerical-inspired instantiations of can-PINN schemes for the convection and pressure gradient terms were derived to solve the incompressible Navier-Stokes (N-S) equations. The superior performance of can-PINNs is demonstrated on several challenging problems, including the flow mixing phenomena, lid driven flow in a cavity, and channel flow over a backward facing step. The results reveal that for challenging problems like these, can-PINNs can consistently achieve very good accuracy whereas conventional AD-based PINNs fail.

Learning in Sinusoidal Spaces with Physics-Informed Neural Networks

A physics-informed neural network (PINN) uses physics-augmented loss functions, e.g., incorporating the residual term from governing differential equations, to ensure its output is consistent with fundamental physics laws. However, it turns out to be difficult to train an accurate PINN model for many problems in practice. In this paper, we address this issue through a novel perspective on the merits of learning in sinusoidal spaces with PINNs. By analyzing asymptotic behavior at model initialization, we first prove that a PINN of increasing size (i.e., width and depth) induces a bias towards flat outputs. Notably, a flat function is a trivial solution to many physics differential equations, hence, deceptively minimizing the residual term of the augmented loss while being far from the true solution. We then show that the sinusoidal mapping of inputs, in an architecture we label as sf-PINN, is able to elevate output variability, thus avoiding being trapped in the deceptive local minimum. In addition, the level of variability can be effectively modulated to match high-frequency patterns in the problem at hand. A key facet of this paper is the comprehensive empirical study that demonstrates the efficacy of learning in sinusoidal spaces with PINNs for a wide range of forward and inverse modelling problems spanning multiple physics domains.