Out-of-Distribution Generalization for Neural Physics Solvers

Neural physics solvers are increasingly used in scientific discovery, given their potential for rapid in silico insights into physical, materials, or biological systems and their long-time evolution. However, poor generalization beyond their training support limits exploration of novel designs and long-time horizon predictions. We introduce NOVA, a route to generalizable neural physics solvers that can provide rapid, accurate solutions to scenarios even under distributional shifts in partial differential equation parameters, geometries and initial conditions. By learning physics-aligned representations from an initial sparse set of scenarios, NOVA consistently achieves 1-2 orders of magnitude lower out-of-distribution errors than data-driven baselines across complex, nonlinear problems including heat transfer, diffusion-reaction and fluid flow. We further showcase NOVA's dual impact on stabilizing long-time dynamical rollouts and improving generative design through application to the simulation of nonlinear Turing systems and fluidic chip optimization. Unlike neural physics solvers that are constrained to retrieval and/or emulation within an a priori space, NOVA enables reliable extrapolation beyond known regimes, a key capability given the need for exploration of novel hypothesis spaces in scientific discovery

Physics-Informed Uncertainty Enables Reliable AI-driven Design

Inverse design is a central goal in much of science and engineering, including frequency-selective surfaces (FSS) that are critical to microelectronics for telecommunications and optical metamaterials. Traditional surrogate-assisted optimization methods using deep learning can accelerate the design process but do not usually incorporate uncertainty quantification, leading to poorer optimization performance due to erroneous predictions in data-sparse regions. Here, we introduce and validate a fundamentally different paradigm of Physics-Informed Uncertainty, where the degree to which a model's prediction violates fundamental physical laws serves as a computationally-cheap and effective proxy for predictive uncertainty. By integrating physics-informed uncertainty into a multi-fidelity uncertainty-aware optimization workflow to design complex frequency-selective surfaces within the 20 - 30 GHz range, we increase the success rate of finding performant solutions from less than 10% to over 50%, while simultaneously reducing computational cost by an order of magnitude compared to the sole use of a high-fidelity solver. These results highlight the necessity of incorporating uncertainty quantification in machine-learning-driven inverse design for high-dimensional problems, and establish physics-informed uncertainty as a viable alternative to quantifying uncertainty in surrogate models for physical systems, thereby setting the stage for autonomous scientific discovery systems that can efficiently and robustly explore and evaluate candidate designs.

Parametric Expensive Multi-Objective Optimization via Generative Solution Modeling

Many real-world applications require solving families of expensive multi-objective optimization problems~(EMOPs) under varying operational conditions. This gives rise to parametric expensive multi-objective optimization problems (P-EMOPs) where each task parameter defines a distinct optimization instance. Current multi-objective Bayesian optimization methods have been widely used for finding finite sets of Pareto optimal solutions for individual tasks. However, P-EMOPs present a fundamental challenge: the continuous task parameter space can contain infinite distinct problems, each requiring separate expensive evaluations. This demands learning an inverse model that can directly predict optimized solutions for any task-preference query without expensive re-evaluation. This paper introduces the first parametric multi-objective Bayesian optimizer that learns this inverse model by alternating between (1) acquisition-driven search leveraging inter-task synergies and (2) generative solution sampling via conditional generative models. This approach enables efficient optimization across related tasks and finally achieves direct solution prediction for unseen parameterized EMOPs without additional expensive evaluations. We theoretically justify the faster convergence by leveraging inter-task synergies through task-aware Gaussian processes. Meanwhile, empirical studies in synthetic and real-world benchmarks further verify the effectiveness of our alternating framework.

Physics-Informed Neuro-Evolution (PINE): A Survey and Prospects

Deep learning models trained on finite data lack a complete understanding of the physical world. On the other hand, physics-informed neural networks (PINNs) are infused with such knowledge through the incorporation of mathematically expressible laws of nature into their training loss function. By complying with physical laws, PINNs provide advantages over purely data-driven models in limited-data regimes. This feature has propelled them to the forefront of scientific machine learning, a domain characterized by scarce and costly data. However, the vision of accurate physics-informed learning comes with significant challenges. This review examines PINNs for the first time in terms of model optimization and generalization, shedding light on the need for new algorithmic advances to overcome issues pertaining to the training speed, precision, and generalizability of today's PINN models. Of particular interest are the gradient-free methods of neuroevolution for optimizing the uniquely complex loss landscapes arising in PINN training. Methods synergizing gradient descent and neuroevolution for discovering bespoke neural architectures and balancing multiple conflicting terms in physics-informed learning objectives are positioned as important avenues for future research. Yet another exciting track is to cast neuroevolution as a meta-learner of generalizable PINN models.

Generalizable Neural Physics Solvers by Baldwinian Evolution

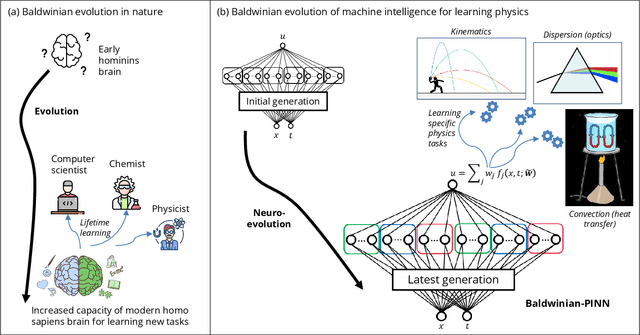
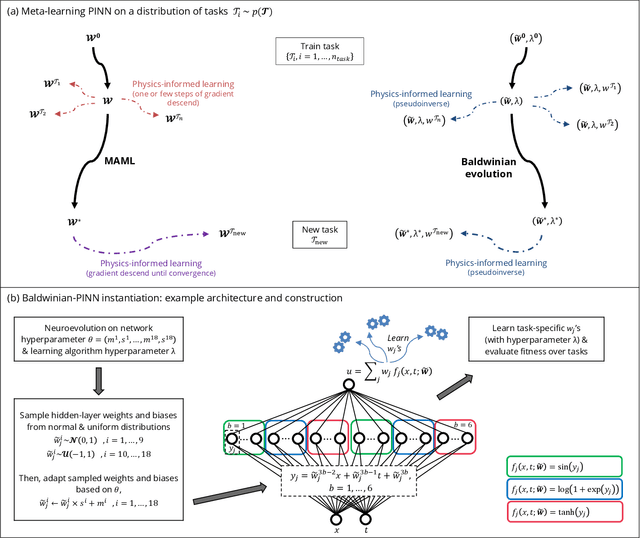
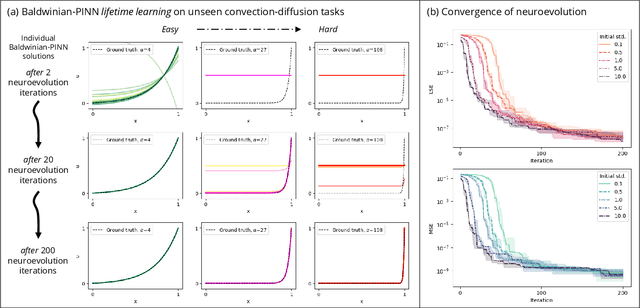
Physics-informed neural networks (PINNs) are at the forefront of scientific machine learning, making possible the creation of machine intelligence that is cognizant of physical laws and able to accurately simulate them. In this paper, the potential of discovering PINNs that generalize over an entire family of physics tasks is studied, for the first time, through a biological lens of the Baldwin effect. Drawing inspiration from the neurodevelopment of precocial species that have evolved to learn, predict and react quickly to their environment, we envision PINNs that are pre-wired with connection strengths inducing strong biases towards efficient learning of physics. To this end, evolutionary selection pressure (guided by proficiency over a family of tasks) is coupled with lifetime learning (to specialize on a smaller subset of those tasks) to produce PINNs that demonstrate fast and physics-compliant prediction capabilities across a range of empirically challenging problem instances. The Baldwinian approach achieves an order of magnitude improvement in prediction accuracy at a fraction of the computation cost compared to state-of-the-art results with PINNs meta-learned by gradient descent. This paper marks a leap forward in the meta-learning of PINNs as generalizable physics solvers.

Graph Neural Network Based Surrogate Model of Physics Simulations for Geometry Design

Computational Intelligence (CI) techniques have shown great potential as a surrogate model of expensive physics simulation, with demonstrated ability to make fast predictions, albeit at the expense of accuracy in some cases. For many scientific and engineering problems involving geometrical design, it is desirable for the surrogate models to precisely describe the change in geometry and predict the consequences. In that context, we develop graph neural networks (GNNs) as fast surrogate models for physics simulation, which allow us to directly train the models on 2/3D geometry designs that are represented by an unstructured mesh or point cloud, without the need for any explicit or hand-crafted parameterization. We utilize an encoder-processor-decoder-type architecture which can flexibly make prediction at both node level and graph level. The performance of our proposed GNN-based surrogate model is demonstrated on 2 example applications: feature designs in the domain of additive engineering and airfoil design in the domain of aerodynamics. The models show good accuracy in their predictions on a separate set of test geometries after training, with almost instant prediction speeds, as compared to O(hour) for the high-fidelity simulations required otherwise.

Automated Quantification of Traffic Particulate Emissions via an Image Analysis Pipeline

Traffic emissions are known to contribute significantly to air pollution around the world, especially in heavily urbanized cities such as Singapore. It has been previously shown that the particulate pollution along major roadways exhibit strong correlation with increased traffic during peak hours, and that reductions in traffic emissions can lead to better health outcomes. However, in many instances, obtaining proper counts of vehicular traffic remains manual and extremely laborious. This then restricts one's ability to carry out longitudinal monitoring for extended periods, for example, when trying to understand the efficacy of intervention measures such as new traffic regulations (e.g. car-pooling) or for computational modelling. Hence, in this study, we propose and implement an integrated machine learning pipeline that utilizes traffic images to obtain vehicular counts that can be easily integrated with other measurements to facilitate various studies. We verify the utility and accuracy of this pipeline on an open-source dataset of traffic images obtained for a location in Singapore and compare the obtained vehicular counts with collocated particulate measurement data obtained over a 2-week period in 2022. The roadside particulate emission is observed to correlate well with obtained vehicular counts with a correlation coefficient of 0.93, indicating that this method can indeed serve as a quick and effective correlate of particulate emissions.

Design of Turing Systems with Physics-Informed Neural Networks

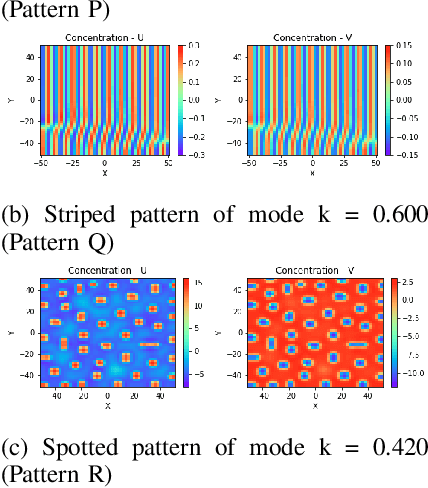
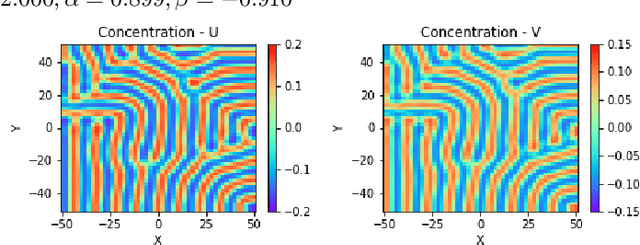
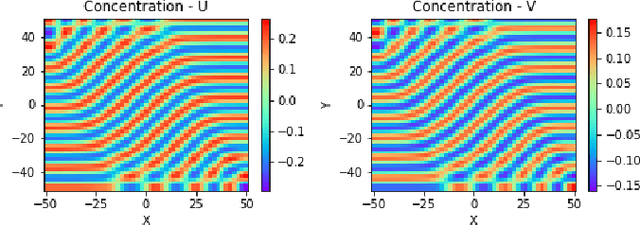
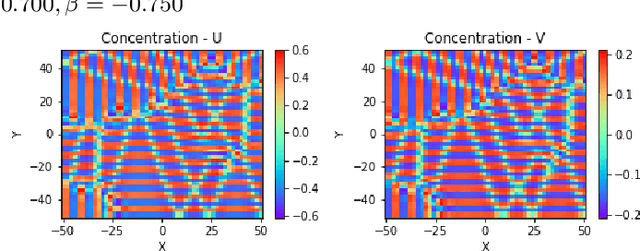
Reaction-diffusion (Turing) systems are fundamental to the formation of spatial patterns in nature and engineering. These systems are governed by a set of non-linear partial differential equations containing parameters that determine the rate of constituent diffusion and reaction. Critically, these parameters, such as diffusion coefficient, heavily influence the mode and type of the final pattern, and quantitative characterization and knowledge of these parameters can aid in bio-mimetic design or understanding of real-world systems. However, the use of numerical methods to infer these parameters can be difficult and computationally expensive. Typically, adjoint solvers may be used, but they are frequently unstable for very non-linear systems. Alternatively, massive amounts of iterative forward simulations are used to find the best match, but this is extremely effortful. Recently, physics-informed neural networks have been proposed as a means for data-driven discovery of partial differential equations, and have seen success in various applications. Thus, we investigate the use of physics-informed neural networks as a tool to infer key parameters in reaction-diffusion systems in the steady-state for scientific discovery or design. Our proof-of-concept results show that the method is able to infer parameters for different pattern modes and types with errors of less than 10\%. In addition, the stochastic nature of this method can be exploited to provide multiple parameter alternatives to the desired pattern, highlighting the versatility of this method for bio-mimetic design. This work thus demonstrates the utility of physics-informed neural networks for inverse parameter inference of reaction-diffusion systems to enhance scientific discovery and design.

FastFlow: AI for Fast Urban Wind Velocity Prediction

Data-driven approaches, including deep learning, have shown great promise as surrogate models across many domains. These extend to various areas in sustainability. An interesting direction for which data-driven methods have not been applied much yet is in the quick quantitative evaluation of urban layouts for planning and design. In particular, urban designs typically involve complex trade-offs between multiple objectives, including limits on urban build-up and/or consideration of urban heat island effect. Hence, it can be beneficial to urban planners to have a fast surrogate model to predict urban characteristics of a hypothetical layout, e.g. pedestrian-level wind velocity, without having to run computationally expensive and time-consuming high-fidelity numerical simulations. This fast surrogate can then be potentially integrated into other design optimization frameworks, including generative models or other gradient-based methods. Here we present the use of CNNs for urban layout characterization that is typically done via high-fidelity numerical simulation. We further apply this model towards a first demonstration of its utility for data-driven pedestrian-level wind velocity prediction. The data set in this work comprises results from high-fidelity numerical simulations of wind velocities for a diverse set of realistic urban layouts, based on randomized samples from a real-world, highly built-up urban city. We then provide prediction results obtained from the trained CNN, demonstrating test errors of under 0.1 m/s for previously unseen urban layouts. We further illustrate how this can be useful for purposes such as rapid evaluation of pedestrian wind velocity for a potential new layout. It is hoped that this data set will further accelerate research in data-driven urban AI, even as our baseline model facilitates quantitative comparison to future methods.

Robustness of Physics-Informed Neural Networks to Noise in Sensor Data

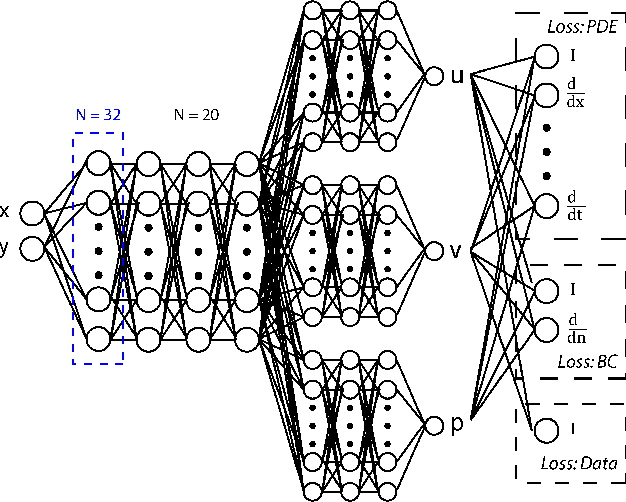
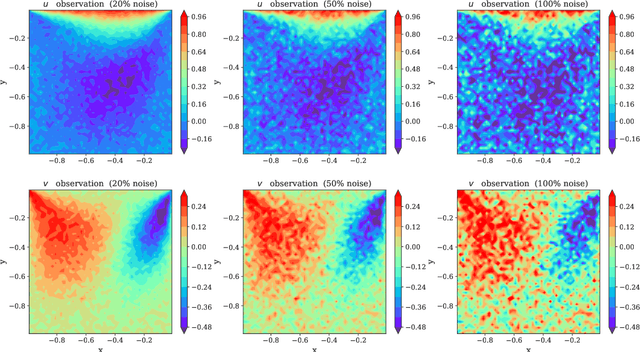
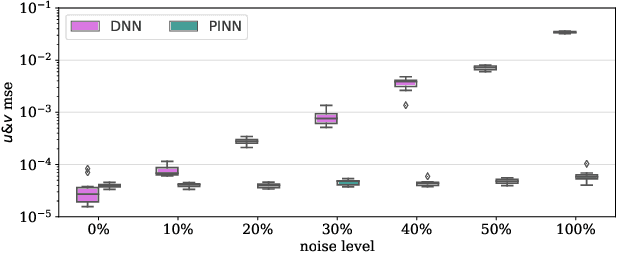
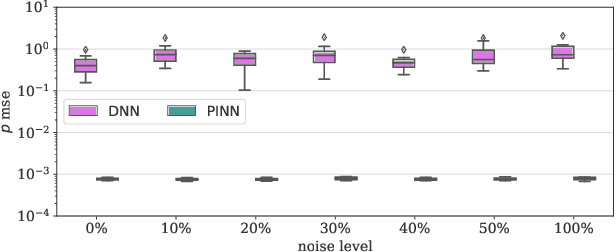
Physics-Informed Neural Networks (PINNs) have been shown to be an effective way of incorporating physics-based domain knowledge into neural network models for many important real-world systems. They have been particularly effective as a means of inferring system information based on data, even in cases where data is scarce. Most of the current work however assumes the availability of high-quality data. In this work, we further conduct a preliminary investigation of the robustness of physics-informed neural networks to the magnitude of noise in the data. Interestingly, our experiments reveal that the inclusion of physics in the neural network is sufficient to negate the impact of noise in data originating from hypothetical low quality sensors with high signal-to-noise ratios of up to 1. The resultant predictions for this test case are seen to still match the predictive value obtained for equivalent data obtained from high-quality sensors with potentially 10x less noise. This further implies the utility of physics-informed neural network modeling for making sense of data from sensor networks in the future, especially with the advent of Industry 4.0 and the increasing trend towards ubiquitous deployment of low-cost sensors which are typically noisier.