U-Net-Based Surrogate Model For Evaluation of Microfluidic Channels

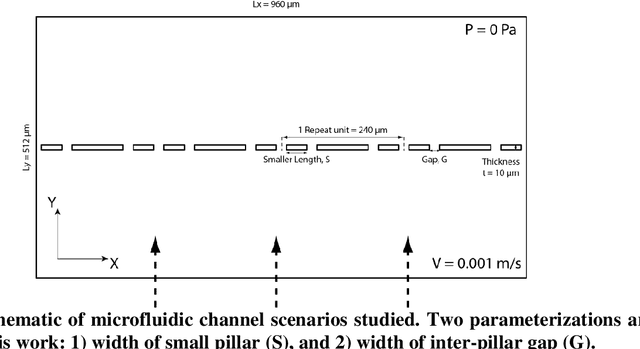
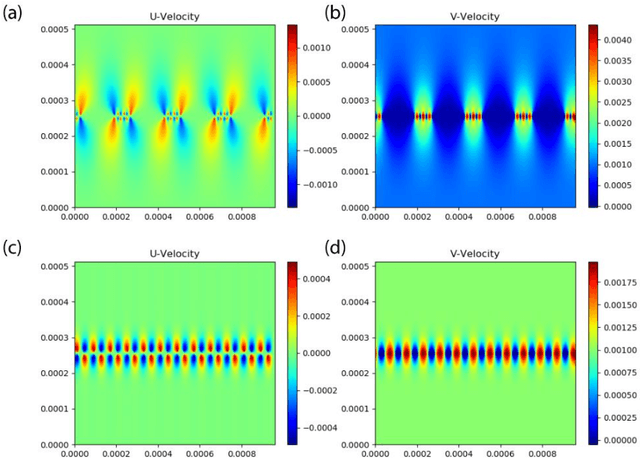
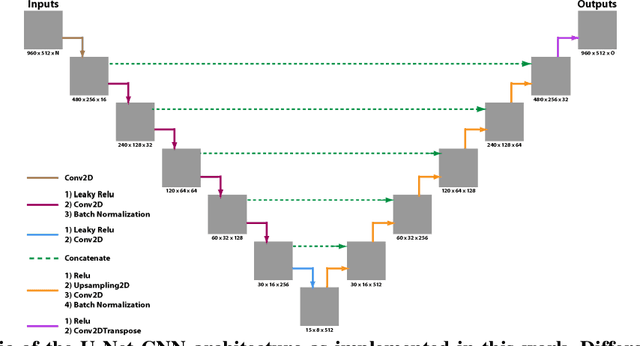
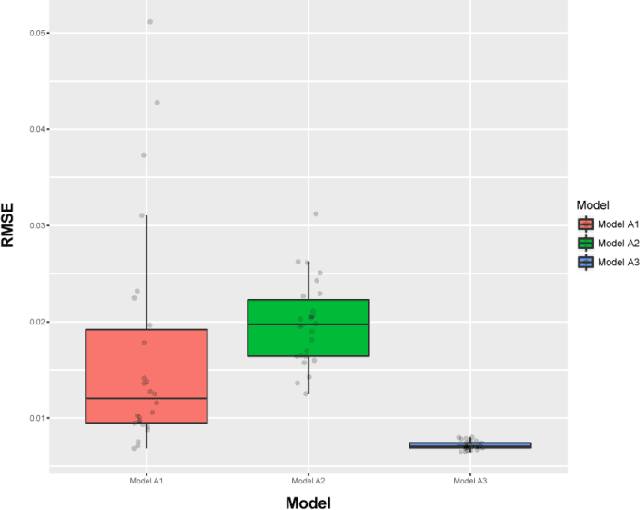
Microfluidics have shown great promise in multiple applications, especially in biomedical diagnostics and separations. While the flow properties of these microfluidic devices can be solved by numerical methods such as computational fluid dynamics (CFD), the process of mesh generation and setting up a numerical solver requires some domain familiarity, while more intuitive commercial programs such as Fluent and StarCCM can be expensive. Hence, in this work, we demonstrated the use of a U-Net convolutional neural network as a surrogate model for predicting the velocity and pressure fields that would result for a particular set of microfluidic filter designs. The surrogate model is fast, easy to set-up and can be used to predict and assess the flow velocity and pressure fields across the domain for new designs of interest via the input of a geometry-encoding matrix. In addition, we demonstrate that the same methodology can also be used to train a network to predict pressure based on velocity data, and propose that this can be an alternative to numerical algorithms for calculating pressure based on velocity measurements from particle-image velocimetry measurements. Critically, in both applications, we demonstrate prediction test errors of less than 1%, suggesting that this is indeed a viable method.

Surrogate Modeling of Fluid Dynamics with a Multigrid Inspired Neural Network Architecture

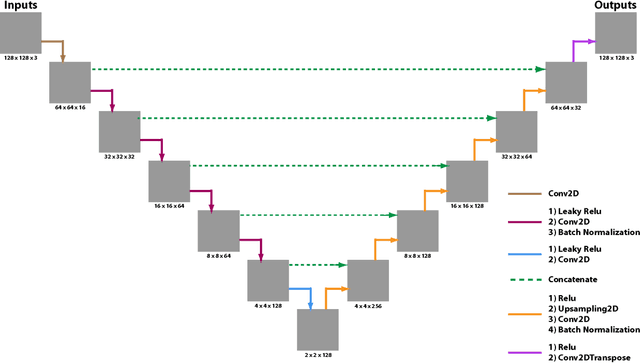
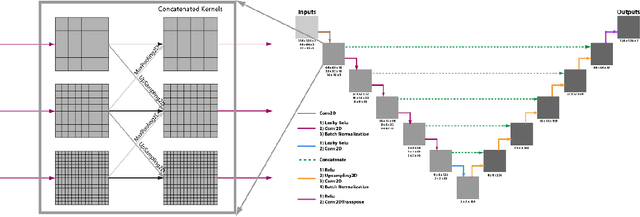
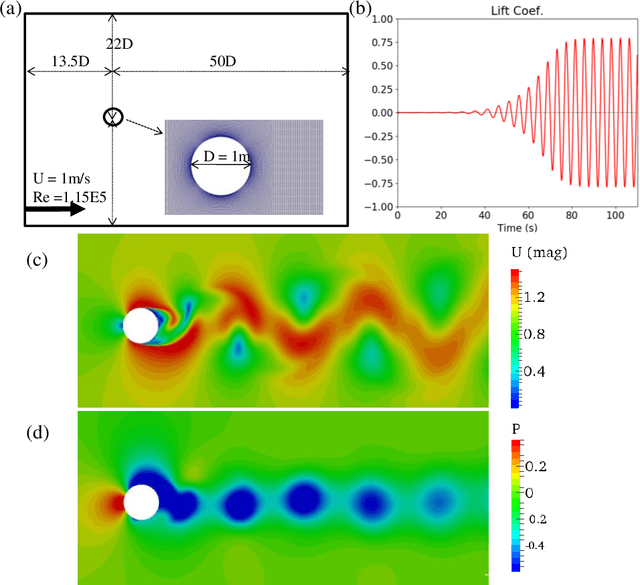
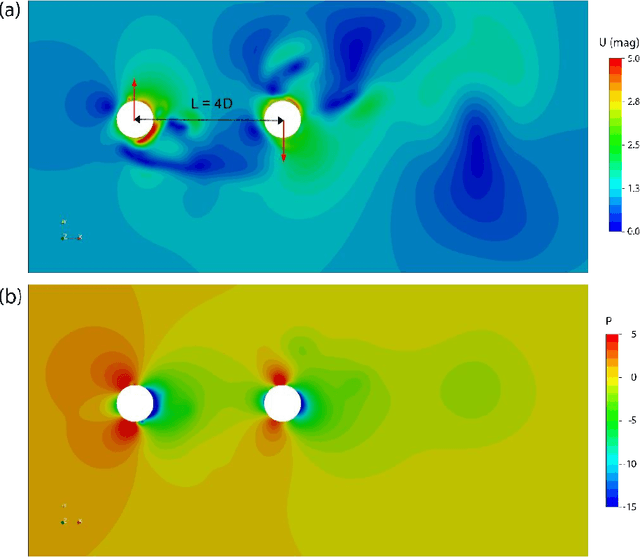
Algebraic or geometric multigrid methods are commonly used in numerical solvers as they are a multi-resolution method able to handle problems with multiple scales. In this work, we propose a modification to the commonly-used U-Net neural network architecture that is inspired by the principles of multigrid methods, referred to here as U-Net-MG. We then demonstrate that this proposed U-Net-MG architecture can successfully reduce the test prediction errors relative to the conventional U-Net architecture when modeling a set of fluid dynamic problems. In total, we demonstrate an improvement in the prediction of velocity and pressure fields for the canonical fluid dynamics cases of flow past a stationary cylinder, flow past 2 cylinders in out-of-phase motion, and flow past an oscillating airfoil in both the propulsion and energy harvesting modes. In general, while both the U-Net and U-Net-MG models can model the systems well with test RMSEs of less than 1%, the use of the U-Net-MG architecture can further reduce RMSEs by between 20% and 70%.