Surrogate Modeling of Fluid Dynamics with a Multigrid Inspired Neural Network Architecture
Paper and Code
May 09, 2021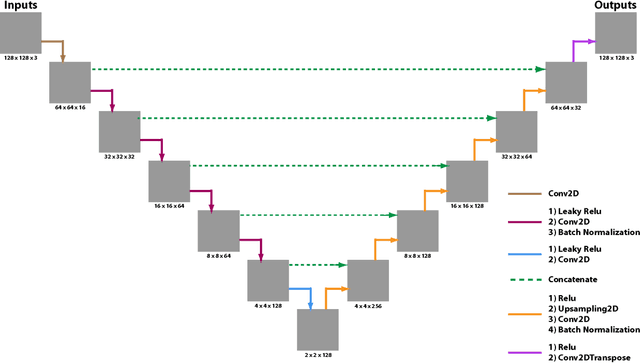
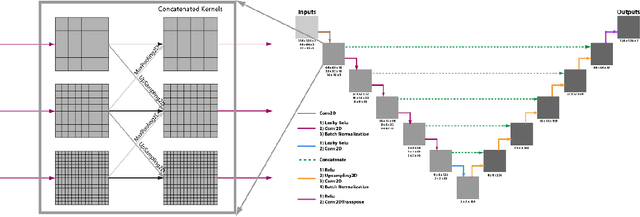
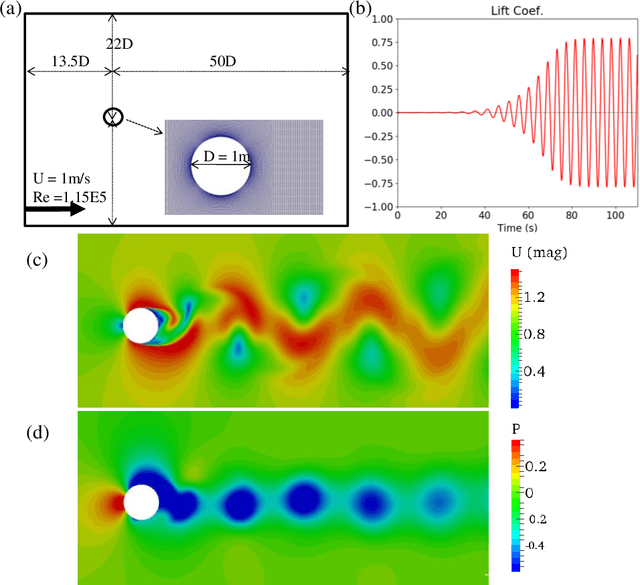
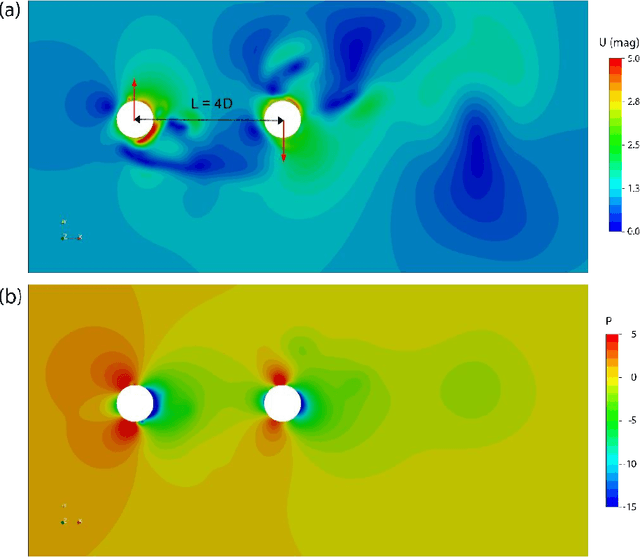
Algebraic or geometric multigrid methods are commonly used in numerical solvers as they are a multi-resolution method able to handle problems with multiple scales. In this work, we propose a modification to the commonly-used U-Net neural network architecture that is inspired by the principles of multigrid methods, referred to here as U-Net-MG. We then demonstrate that this proposed U-Net-MG architecture can successfully reduce the test prediction errors relative to the conventional U-Net architecture when modeling a set of fluid dynamic problems. In total, we demonstrate an improvement in the prediction of velocity and pressure fields for the canonical fluid dynamics cases of flow past a stationary cylinder, flow past 2 cylinders in out-of-phase motion, and flow past an oscillating airfoil in both the propulsion and energy harvesting modes. In general, while both the U-Net and U-Net-MG models can model the systems well with test RMSEs of less than 1%, the use of the U-Net-MG architecture can further reduce RMSEs by between 20% and 70%.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge