Ji Oon Lee
Detection problems in the spiked matrix models
Jan 16, 2023Abstract:We study the statistical decision process of detecting the low-rank signal from various signal-plus-noise type data matrices, known as the spiked random matrix models. We first show that the principal component analysis can be improved by entrywise pre-transforming the data matrix if the noise is non-Gaussian, generalizing the known results for the spiked random matrix models with rank-1 signals. As an intermediate step, we find out sharp phase transition thresholds for the extreme eigenvalues of spiked random matrices, which generalize the Baik-Ben Arous-P\'{e}ch\'{e} (BBP) transition. We also prove the central limit theorem for the linear spectral statistics for the spiked random matrices and propose a hypothesis test based on it, which does not depend on the distribution of the signal or the noise. When the noise is non-Gaussian noise, the test can be improved with an entrywise transformation to the data matrix with additive noise. We also introduce an algorithm that estimates the rank of the signal when it is not known a priori.
Asymptotic Normality of Log Likelihood Ratio and Fundamental Limit of the Weak Detection for Spiked Wigner Matrices
Mar 02, 2022
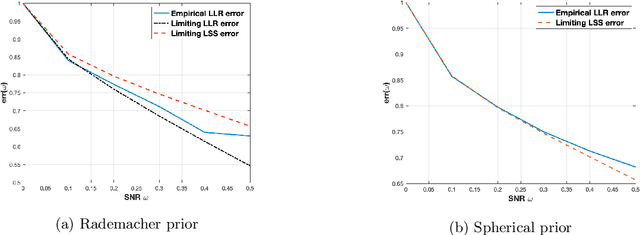
Abstract:We consider the problem of detecting the presence of a signal in a rank-one spiked Wigner model. Assuming that the signal is drawn from the Rademacher prior, we prove that the log likelihood ratio of the spiked model against the null model converges to a Gaussian when the signal-to-noise ratio is below a certain threshold. From the mean and the variance of the limiting Gaussian, we also compute the limit of the sum of the Type-I error and the Type-II error of the likelihood ratio test.
Detection of Signal in the Spiked Rectangular Models
Apr 28, 2021
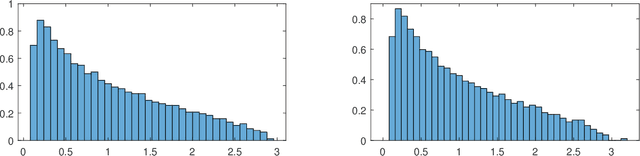
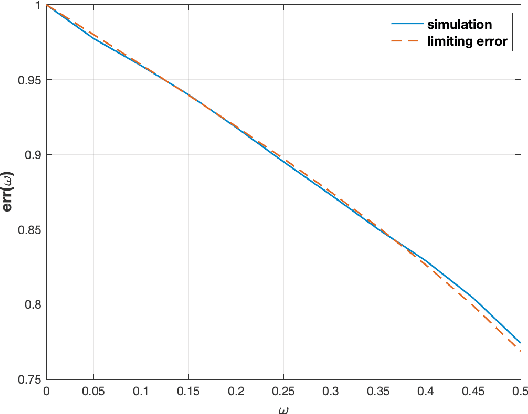
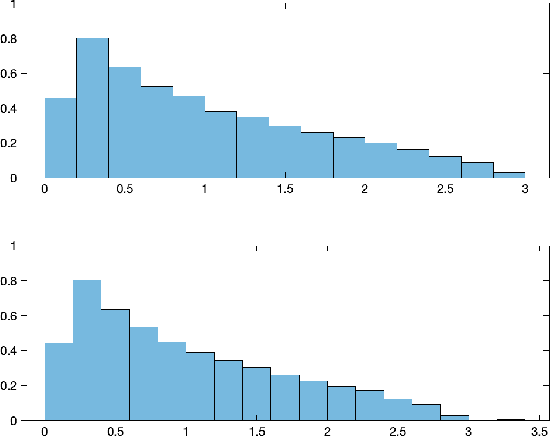
Abstract:We consider the problem of detecting signals in the rank-one signal-plus-noise data matrix models that generalize the spiked Wishart matrices. We show that the principal component analysis can be improved by pre-transforming the matrix entries if the noise is non-Gaussian. As an intermediate step, we prove a sharp phase transition of the largest eigenvalues of spiked rectangular matrices, which extends the Baik-Ben Arous-P\'ech\'e (BBP) transition. We also propose a hypothesis test to detect the presence of signal with low computational complexity, based on the linear spectral statistics, which minimizes the sum of the Type-I and Type-II errors when the noise is Gaussian.
Weak Detection in the Spiked Wigner Model with General Rank
Jan 16, 2020
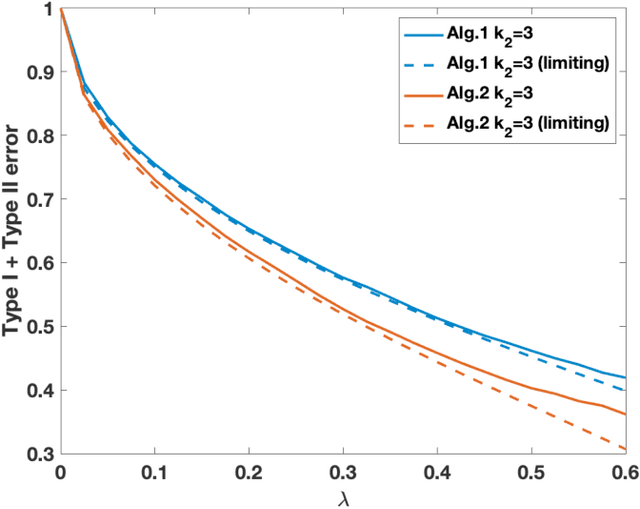

Abstract:We study the statistical decision process of detecting the presence of signal from a 'signal+noise' type matrix model with an additive Wigner noise. We derive the error of the likelihood ratio test, which minimizes the sum of the Type-I and Type-II errors, under the Gaussian noise for the signal matrix with arbitrary finite rank. We propose a hypothesis test based on the linear spectral statistics of the data matrix, which is optimal and does not depend on the distribution of the signal or the noise. We also introduce a test for rank estimation that does not require the prior information on the rank of the signal.
Weak detection of signal in the spiked Wigner model
Sep 28, 2018

Abstract:We consider the problem of detecting the presence of the signal in a rank-one signal-plus-noise data matrix. In case the signal-to-noise ratio is under a certain threshold, we propose a hypothesis testing based on the linear spectral statistics of the data matrix. The error of the proposed test matches that of the likelihood ratio test, which minimizes the sum of the Type-I and Type-II errors. The test does not depend on the distribution of the signal or the noise, and it can be extended to an adaptive test, which does not require the knowledge on the value of the signal-to-noise ratio, but performs better than random guess. As an intermediate step, we establish a central limit theorem for the linear spectral statistics of rank-one spiked Wigner matrices for a general spike.
Parity Crowdsourcing for Cooperative Labeling
Sep 04, 2018



Abstract:Consider a database of $k$ objects, e.g., a set of videos, where each object has a binary attribute, e.g., a video's suitability for children. The attributes of the objects are to be determined under a crowdsourcing model: a worker is queried about the labels of a chosen subset of objects and either responds with a correct binary answer or declines to respond. Here we propose a parity response model: the worker is asked to check whether the number of objects having a given attribute in the chosen subset is even or odd. For example, if the subset includes two objects, the worker checks whether the two belong to the same class or not. We propose a method for designing the sequence of subsets of objects to be queried so that the attributes of the objects can be identified with high probability using few ($n$) answers. The method is based on an analogy to the design of Fountain codes for erasure channels. We define the query difficulty $\bar{d}$ as the average size of the query subsets and we define the sample complexity $n$ as the minimum number of collected answers required to attain a given recovery accuracy. We obtain fundamental tradeoffs between recovery accuracy, query difficulty, and sample complexity. In particular, the necessary and sufficient sample complexity required for recovering all $k$ attributes with high probability is $n = c_0 \max\{k, (k \log k)/\bar{d}\}$ and the sample complexity for recovering a fixed proportion $(1-\delta)k$ of the attributes for $\delta=o(1)$ is $n = c_1\max\{k, (k \log(1/\delta))/\bar{d}\}$, where $c_0, c_1>0$.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge