Detection of Signal in the Spiked Rectangular Models
Paper and Code
Apr 28, 2021
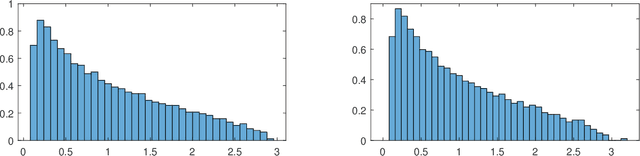
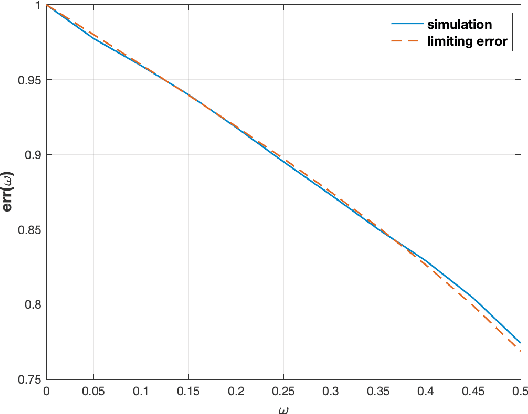
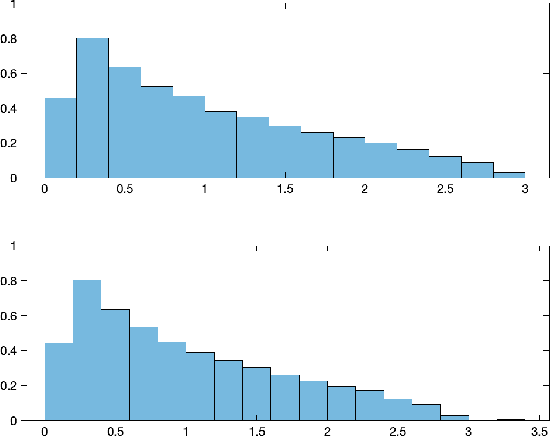
We consider the problem of detecting signals in the rank-one signal-plus-noise data matrix models that generalize the spiked Wishart matrices. We show that the principal component analysis can be improved by pre-transforming the matrix entries if the noise is non-Gaussian. As an intermediate step, we prove a sharp phase transition of the largest eigenvalues of spiked rectangular matrices, which extends the Baik-Ben Arous-P\'ech\'e (BBP) transition. We also propose a hypothesis test to detect the presence of signal with low computational complexity, based on the linear spectral statistics, which minimizes the sum of the Type-I and Type-II errors when the noise is Gaussian.
* 38 pages, 6 figures
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge