Detection problems in the spiked matrix models

We study the statistical decision process of detecting the low-rank signal from various signal-plus-noise type data matrices, known as the spiked random matrix models. We first show that the principal component analysis can be improved by entrywise pre-transforming the data matrix if the noise is non-Gaussian, generalizing the known results for the spiked random matrix models with rank-1 signals. As an intermediate step, we find out sharp phase transition thresholds for the extreme eigenvalues of spiked random matrices, which generalize the Baik-Ben Arous-P\'{e}ch\'{e} (BBP) transition. We also prove the central limit theorem for the linear spectral statistics for the spiked random matrices and propose a hypothesis test based on it, which does not depend on the distribution of the signal or the noise. When the noise is non-Gaussian noise, the test can be improved with an entrywise transformation to the data matrix with additive noise. We also introduce an algorithm that estimates the rank of the signal when it is not known a priori.

Detection of Signal in the Spiked Rectangular Models

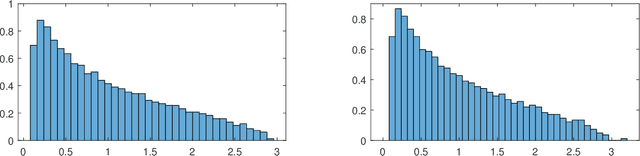
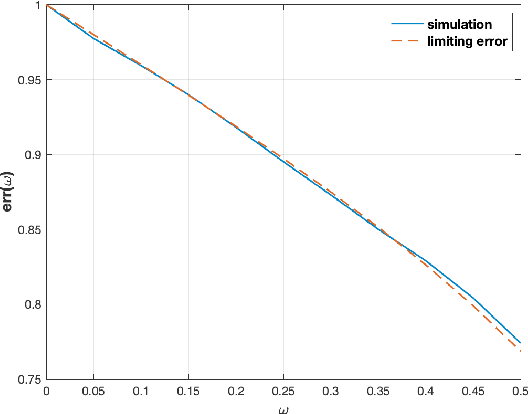
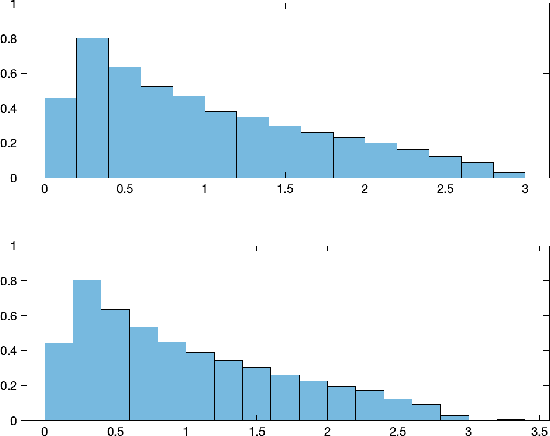
We consider the problem of detecting signals in the rank-one signal-plus-noise data matrix models that generalize the spiked Wishart matrices. We show that the principal component analysis can be improved by pre-transforming the matrix entries if the noise is non-Gaussian. As an intermediate step, we prove a sharp phase transition of the largest eigenvalues of spiked rectangular matrices, which extends the Baik-Ben Arous-P\'ech\'e (BBP) transition. We also propose a hypothesis test to detect the presence of signal with low computational complexity, based on the linear spectral statistics, which minimizes the sum of the Type-I and Type-II errors when the noise is Gaussian.

Weak Detection in the Spiked Wigner Model with General Rank

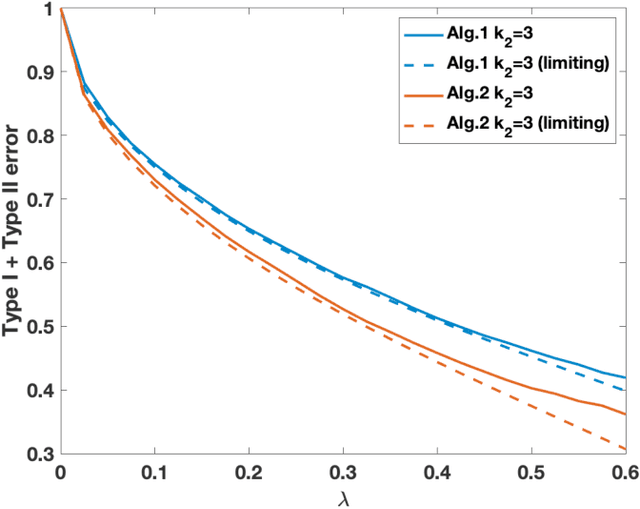
We study the statistical decision process of detecting the presence of signal from a 'signal+noise' type matrix model with an additive Wigner noise. We derive the error of the likelihood ratio test, which minimizes the sum of the Type-I and Type-II errors, under the Gaussian noise for the signal matrix with arbitrary finite rank. We propose a hypothesis test based on the linear spectral statistics of the data matrix, which is optimal and does not depend on the distribution of the signal or the noise. We also introduce a test for rank estimation that does not require the prior information on the rank of the signal.