Weak Detection in the Spiked Wigner Model with General Rank

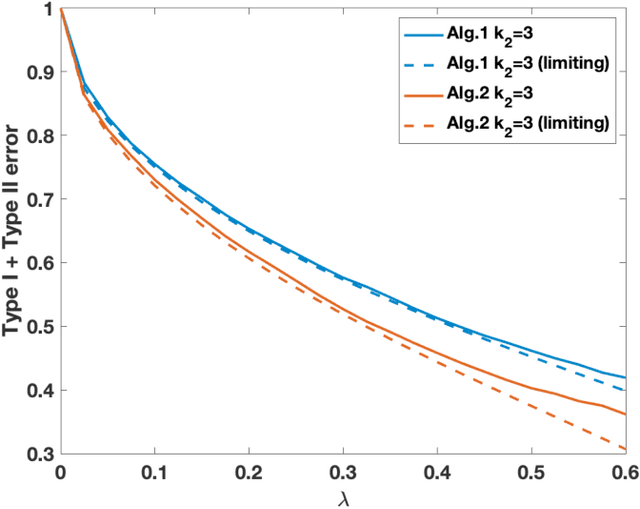
We study the statistical decision process of detecting the presence of signal from a 'signal+noise' type matrix model with an additive Wigner noise. We derive the error of the likelihood ratio test, which minimizes the sum of the Type-I and Type-II errors, under the Gaussian noise for the signal matrix with arbitrary finite rank. We propose a hypothesis test based on the linear spectral statistics of the data matrix, which is optimal and does not depend on the distribution of the signal or the noise. We also introduce a test for rank estimation that does not require the prior information on the rank of the signal.