Dynamic Tree Databases in Automated Planning

A central challenge in scaling up explicit state-space search for large tasks is compactly representing the set of generated states. Tree databases, a data structure from model checking, require constant space per generated state in the best case, but they need a large preallocation of memory. We propose a novel dynamic variant of tree databases for compressing state sets over propositional and numeric variables and prove that it maintains the desirable properties of the static counterpart. Our empirical evaluation of state compression techniques for grounded and lifted planning on classical and numeric planning tasks reveals compression ratios of several orders of magnitude, often with negligible runtime overhead.

The 2025 Planning Performance of Frontier Large Language Models

The capacity of Large Language Models (LLMs) for reasoning remains an active area of research, with the capabilities of frontier models continually advancing. We provide an updated evaluation of the end-to-end planning performance of three frontier LLMs as of 2025, where models are prompted to generate a plan from PDDL domain and task descriptions. We evaluate DeepSeek R1, Gemini 2.5 Pro, GPT-5 and as reference the planner LAMA on a subset of domains from the most recent Learning Track of the International Planning Competition. Our results show that on standard PDDL domains, the performance of GPT-5 in terms of solved tasks is competitive with LAMA. When the PDDL domains and tasks are obfuscated to test for pure reasoning, the performance of all LLMs degrades, though less severely than previously reported for other models. These results show substantial improvements over prior generations of LLMs, reducing the performance gap to planners on a challenging benchmark.

Symmetry-Aware Transformer Training for Automated Planning

While transformers excel in many settings, their application in the field of automated planning is limited. Prior work like PlanGPT, a state-of-the-art decoder-only transformer, struggles with extrapolation from easy to hard planning problems. This in turn stems from problem symmetries: planning tasks can be represented with arbitrary variable names that carry no meaning beyond being identifiers. This causes a combinatorial explosion of equivalent representations that pure transformers cannot efficiently learn from. We propose a novel contrastive learning objective to make transformers symmetry-aware and thereby compensate for their lack of inductive bias. Combining this with architectural improvements, we show that transformers can be efficiently trained for either plan-generation or heuristic-prediction. Our results across multiple planning domains demonstrate that our symmetry-aware training effectively and efficiently addresses the limitations of PlanGPT.

Classical Planning with LLM-Generated Heuristics: Challenging the State of the Art with Python Code

In recent years, large language models (LLMs) have shown remarkable capabilities in various artificial intelligence problems. However, they fail to plan reliably, even when prompted with a detailed definition of the planning task. Attempts to improve their planning capabilities, such as chain-of-thought prompting, fine-tuning, and explicit "reasoning" still yield incorrect plans and usually fail to generalize to larger tasks. In this paper, we show how to use LLMs to generate correct plans, even for out-of-distribution tasks of increasing size. For a given planning domain, we ask an LLM to generate several domain-dependent heuristic functions in the form of Python code, evaluate them on a set of training tasks within a greedy best-first search, and choose the strongest one. The resulting LLM-generated heuristics solve many more unseen test tasks than state-of-the-art domain-independent heuristics for classical planning. They are even competitive with the strongest learning algorithm for domain-dependent planning. These findings are especially remarkable given that our proof-of-concept implementation is based on an unoptimized Python planner and the baselines all build upon highly optimized C++ code. In some domains, the LLM-generated heuristics expand fewer states than the baselines, revealing that they are not only efficiently computable, but sometimes even more informative than the state-of-the-art heuristics. Overall, our results show that sampling a set of planning heuristic function programs can significantly improve the planning capabilities of LLMs.

NL2Plan: Robust LLM-Driven Planning from Minimal Text Descriptions

Today's classical planners are powerful, but modeling input tasks in formats such as PDDL is tedious and error-prone. In contrast, planning with Large Language Models (LLMs) allows for almost any input text, but offers no guarantees on plan quality or even soundness. In an attempt to merge the best of these two approaches, some work has begun to use LLMs to automate parts of the PDDL creation process. However, these methods still require various degrees of expert input. We present NL2Plan, the first domain-agnostic offline LLM-driven planning system. NL2Plan uses an LLM to incrementally extract the necessary information from a short text prompt before creating a complete PDDL description of both the domain and the problem, which is finally solved by a classical planner. We evaluate NL2Plan on four planning domains and find that it solves 10 out of 15 tasks - a clear improvement over a plain chain-of-thought reasoning LLM approach, which only solves 2 tasks. Moreover, in two out of the five failure cases, instead of returning an invalid plan, NL2Plan reports that it failed to solve the task. In addition to using NL2Plan in end-to-end mode, users can inspect and correct all of its intermediate results, such as the PDDL representation, increasing explainability and making it an assistive tool for PDDL creation.

Numeric Reward Machines

Reward machines inform reinforcement learning agents about the reward structure of the environment and often drastically speed up the learning process. However, reward machines only accept Boolean features such as robot-reached-gold. Consequently, many inherently numeric tasks cannot profit from the guidance offered by reward machines. To address this gap, we aim to extend reward machines with numeric features such as distance-to-gold. For this, we present two types of reward machines: numeric-Boolean and numeric. In a numeric-Boolean reward machine, distance-to-gold is emulated by two Boolean features distance-to-gold-decreased and robot-reached-gold. In a numeric reward machine, distance-to-gold is used directly alongside the Boolean feature robot-reached-gold. We compare our new approaches to a baseline reward machine in the Craft domain, where the numeric feature is the agent-to-target distance. We use cross-product Q-learning, Q-learning with counter-factual experiences, and the options framework for learning. Our experimental results show that our new approaches significantly outperform the baseline approach. Extending reward machines with numeric features opens up new possibilities of using reward machines in inherently numeric tasks.

Consolidating LAMA with Best-First Width Search

One key decision for heuristic search algorithms is how to balance exploration and exploitation. In classical planning, novelty search has come out as the most successful approach in this respect. The idea is to favor states that contain previously unseen facts when searching for a plan. This is done by maintaining a record of the tuples of facts observed in previous states. Then the novelty of a state is the size of the smallest previously unseen tuple. The most successful version of novelty search is best-first width search (BFWS), which combines novelty measures with heuristic estimates. An orthogonal approach to balance exploration-exploitation is to use several open-lists. These open-lists are ordered using different heuristic estimates, which diversify the information used in the search. The search algorithm then alternates between these open-lists, trying to exploit these different estimates. This is the approach used by LAMA, a classical planner that, a decade after its release, is still considered state-of-the-art in agile planning. In this paper, we study how to combine LAMA and BFWS. We show that simply adding the strongest open-list used in BFWS to LAMA harms performance. However, we show that combining only parts of each planner leads to a new state-of-the-art agile planner.

Learning Sketches for Decomposing Planning Problems into Subproblems of Bounded Width: Extended Version

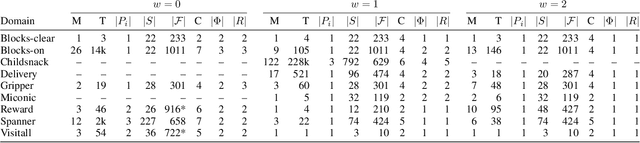
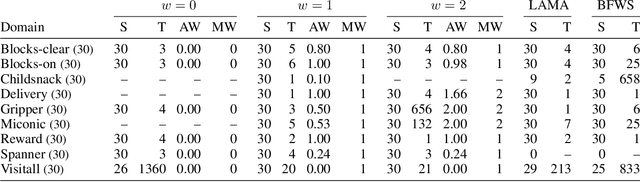
Recently, sketches have been introduced as a general language for representing the subgoal structure of instances drawn from the same domain. Sketches are collections of rules of the form C -> E over a given set of features where C expresses Boolean conditions and E expresses qualitative changes. Each sketch rule defines a subproblem: going from a state that satisfies C to a state that achieves the change expressed by E or a goal state. Sketches can encode simple goal serializations, general policies, or decompositions of bounded width that can be solved greedily, in polynomial time, by the SIW_R variant of the SIW algorithm. Previous work has shown the computational value of sketches over benchmark domains that, while tractable, are challenging for domain-independent planners. In this work, we address the problem of learning sketches automatically given a planning domain, some instances of the target class of problems, and the desired bound on the sketch width. We present a logical formulation of the problem, an implementation using the ASP solver Clingo, and experimental results. The sketch learner and the SIW_R planner yield a domain-independent planner that learns and exploits domain structure in a crisp and explicit form.

Expressing and Exploiting the Common Subgoal Structure of Classical Planning Domains Using Sketches: Extended Version

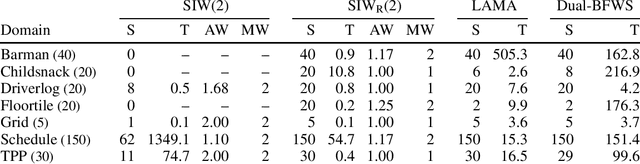
Width-based planning methods exploit the use of conjunctive goals for decomposing problems into subproblems of low width. However, algorithms like SIW fail when the goal is not serializable. In this work, we address this limitation of SIW by using a simple but powerful language for expressing problem decompositions introduced recently by Bonet and Geffner, called policy sketches. A policy sketch R consists of a set of Boolean and numerical features and a set of sketch rules that express how the values of these features are supposed to change. Like general policies, policy sketches are domain general, but unlike policies, the changes captured by sketch rules do not need to be achieved in a single step. We show that many planning domains that cannot be solved by SIW are provably solvable in low polynomial time with the SIW_R algorithm, the version of SIW that employs user-provided policy sketches. Policy sketches are thus shown to be a powerful language for expressing domain-specific knowledge in a simple and compact way and a convenient alternative to languages such as HTNs or temporal logics. Furthermore, policy sketches make it easy to express general problem decompositions and prove key properties like their complexity and width.