Learning General Policies with Policy Gradient Methods

While reinforcement learning methods have delivered remarkable results in a number of settings, generalization, i.e., the ability to produce policies that generalize in a reliable and systematic way, has remained a challenge. The problem of generalization has been addressed formally in classical planning where provable correct policies that generalize over all instances of a given domain have been learned using combinatorial methods. The aim of this work is to bring these two research threads together to illuminate the conditions under which (deep) reinforcement learning approaches, and in particular, policy optimization methods, can be used to learn policies that generalize like combinatorial methods do. We draw on lessons learned from previous combinatorial and deep learning approaches, and extend them in a convenient way. From the former, we model policies as state transition classifiers, as (ground) actions are not general and change from instance to instance. From the latter, we use graph neural networks (GNNs) adapted to deal with relational structures for representing value functions over planning states, and in our case, policies. With these ingredients in place, we find that actor-critic methods can be used to learn policies that generalize almost as well as those obtained using combinatorial approaches while avoiding the scalability bottleneck and the use of feature pools. Moreover, the limitations of the DRL methods on the benchmarks considered have little to do with deep learning or reinforcement learning algorithms, and result from the well-understood expressive limitations of GNNs, and the tradeoff between optimality and generalization (general policies cannot be optimal in some domains). Both of these limitations are addressed without changing the basic DRL methods by adding derived predicates and an alternative cost structure to optimize.

First-Order Representation Languages for Goal-Conditioned RL

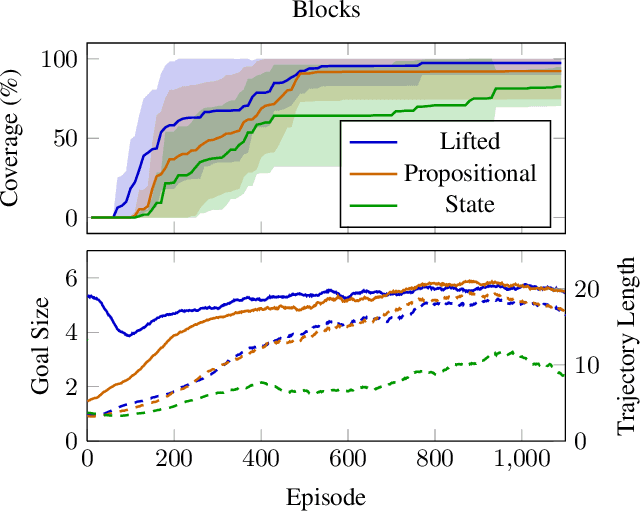
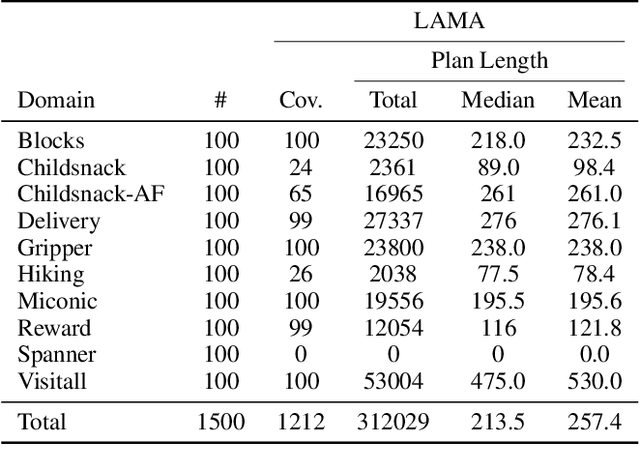
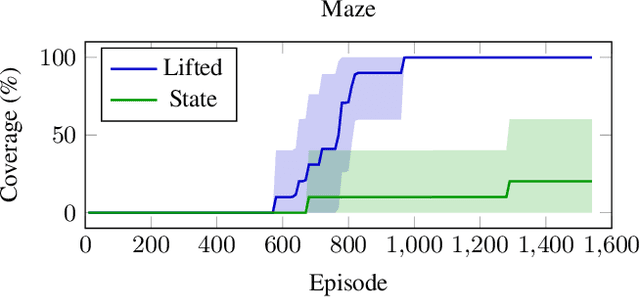
First-order relational languages have been used in MDP planning and reinforcement learning (RL) for two main purposes: specifying MDPs in compact form, and representing and learning policies that are general and not tied to specific instances or state spaces. In this work, we instead consider the use of first-order languages in goal-conditioned RL and generalized planning. The question is how to learn goal-conditioned and general policies when the training instances are large and the goal cannot be reached by random exploration alone. The technique of Hindsight Experience Replay (HER) provides an answer to this question: it relabels unsuccessful trajectories as successful ones by replacing the original goal with one that was actually achieved. If the target policy must generalize across states and goals, trajectories that do not reach the original goal states can enable more data- and time-efficient learning. In this work, we show that further performance gains can be achieved when states and goals are represented by sets of atoms. We consider three versions: goals as full states, goals as subsets of the original goals, and goals as lifted versions of these subgoals. The result is that the latter two successfully learn general policies on large planning instances with sparse rewards by automatically creating a curriculum of easier goals of increasing complexity. The experiments illustrate the computational gains of these versions, their limitations, and opportunities for addressing them.

Learning Sketch Decompositions in Planning via Deep Reinforcement Learning

In planning and reinforcement learning, the identification of common subgoal structures across problems is important when goals are to be achieved over long horizons. Recently, it has been shown that such structures can be expressed as feature-based rules, called sketches, over a number of classical planning domains. These sketches split problems into subproblems which then become solvable in low polynomial time by a greedy sequence of IW$(k)$ searches. Methods for learning sketches using feature pools and min-SAT solvers have been developed, yet they face two key limitations: scalability and expressivity. In this work, we address these limitations by formulating the problem of learning sketch decompositions as a deep reinforcement learning (DRL) task, where general policies are sought in a modified planning problem where the successor states of a state s are defined as those reachable from s through an IW$(k)$ search. The sketch decompositions obtained through this method are experimentally evaluated across various domains, and problems are regarded as solved by the decomposition when the goal is reached through a greedy sequence of IW$(k)$ searches. While our DRL approach for learning sketch decompositions does not yield interpretable sketches in the form of rules, we demonstrate that the resulting decompositions can often be understood in a crisp manner.

Learning Lifted STRIPS Models from Action Traces Alone: A Simple, General, and Scalable Solution

Learning STRIPS action models from action traces alone is a challenging problem as it involves learning the domain predicates as well. In this work, a novel approach is introduced which, like the well-known LOCM systems, is scalable, but like SAT approaches, is sound and complete. Furthermore, the approach is general and imposes no restrictions on the hidden domain or the number or arity of the predicates. The new learning method is based on an \emph{efficient, novel test} that checks whether the assumption that a predicate is affected by a set of action patterns, namely, actions with specific argument positions, is consistent with the traces. The predicates and action patterns that pass the test provide the basis for the learned domain that is then easily completed with preconditions and static predicates. The new method is studied theoretically and experimentally. For the latter, the method is evaluated on traces and graphs obtained from standard classical domains like the 8-puzzle, which involve hundreds of thousands of states and transitions. The learned representations are then verified on larger instances.

Learning to Ground Existentially Quantified Goals

Goal instructions for autonomous AI agents cannot assume that objects have unique names. Instead, objects in goals must be referred to by providing suitable descriptions. However, this raises problems in both classical planning and generalized planning. The standard approach to handling existentially quantified goals in classical planning involves compiling them into a DNF formula that encodes all possible variable bindings and adding dummy actions to map each DNF term into the new, dummy goal. This preprocessing is exponential in the number of variables. In generalized planning, the problem is different: even if general policies can deal with any initial situation and goal, executing a general policy requires the goal to be grounded to define a value for the policy features. The problem of grounding goals, namely finding the objects to bind the goal variables, is subtle: it is a generalization of classical planning, which is a special case when there are no goal variables to bind, and constraint reasoning, which is a special case when there are no actions. In this work, we address the goal grounding problem with a novel supervised learning approach. A GNN architecture, trained to predict the cost of partially quantified goals over small domain instances is tested on larger instances involving more objects and different quantified goals. The proposed architecture is evaluated experimentally over several planning domains where generalization is tested along several dimensions including the number of goal variables and objects that can bind such variables. The scope of the approach is also discussed in light of the known relationship between GNNs and C2 logics.

Symmetries and Expressive Requirements for Learning General Policies

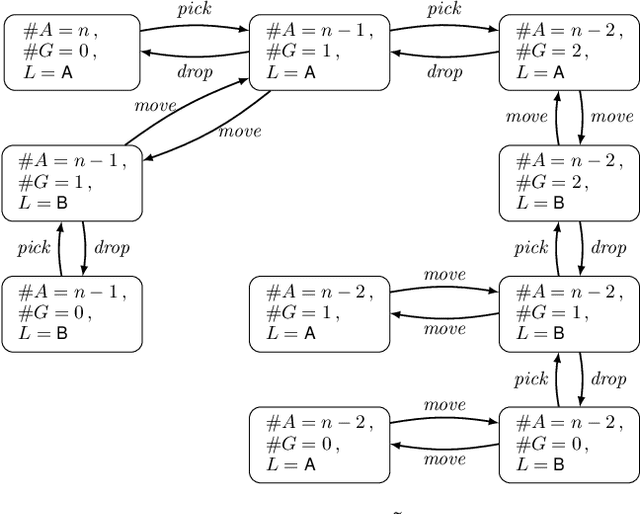
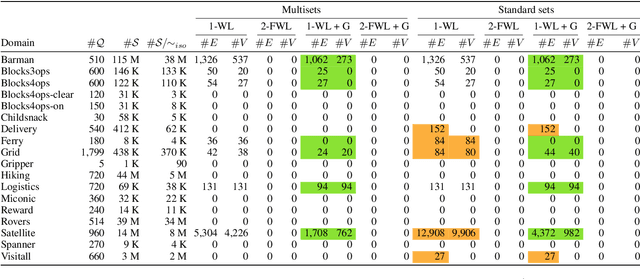
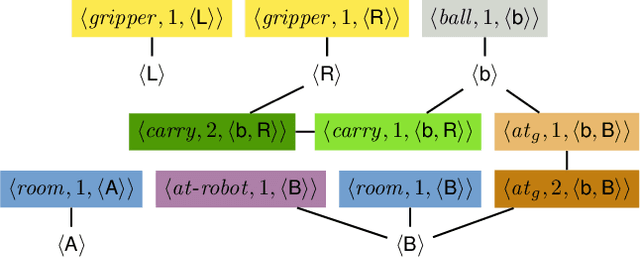
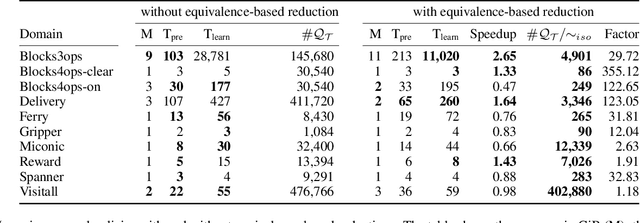
State symmetries play an important role in planning and generalized planning. In the first case, state symmetries can be used to reduce the size of the search; in the second, to reduce the size of the training set. In the case of general planning, however, it is also critical to distinguish non-symmetric states, i.e., states that represent non-isomorphic relational structures. However, while the language of first-order logic distinguishes non-symmetric states, the languages and architectures used to represent and learn general policies do not. In particular, recent approaches for learning general policies use state features derived from description logics or learned via graph neural networks (GNNs) that are known to be limited by the expressive power of C_2, first-order logic with two variables and counting. In this work, we address the problem of detecting symmetries in planning and generalized planning and use the results to assess the expressive requirements for learning general policies over various planning domains. For this, we map planning states to plain graphs, run off-the-shelf algorithms to determine whether two states are isomorphic with respect to the goal, and run coloring algorithms to determine if C_2 features computed logically or via GNNs distinguish non-isomorphic states. Symmetry detection results in more effective learning, while the failure to detect non-symmetries prevents general policies from being learned at all in certain domains.

Learning Generalized Policies for Fully Observable Non-Deterministic Planning Domains

General policies represent reactive strategies for solving large families of planning problems like the infinite collection of solvable instances from a given domain. Methods for learning such policies from a collection of small training instances have been developed successfully for classical domains. In this work, we extend the formulations and the resulting combinatorial methods for learning general policies over fully observable, non-deterministic (FOND) domains. We also evaluate the resulting approach experimentally over a number of benchmark domains in FOND planning, present the general policies that result in some of these domains, and prove their correctness. The method for learning general policies for FOND planning can actually be seen as an alternative FOND planning method that searches for solutions, not in the given state space but in an abstract space defined by features that must be learned as well.

On Policy Reuse: An Expressive Language for Representing and Executing General Policies that Call Other Policies

Recently, a simple but powerful language for expressing and learning general policies and problem decompositions (sketches) has been introduced in terms of rules defined over a set of Boolean and numerical features. In this work, we consider three extensions of this language aimed at making policies and sketches more flexible and reusable: internal memory states, as in finite state controllers; indexical features, whose values are a function of the state and a number of internal registers that can be loaded with objects; and modules that wrap up policies and sketches and allow them to call each other by passing parameters. In addition, unlike general policies that select state transitions rather than ground actions, the new language allows for the selection of such actions. The expressive power of the resulting language for policies and sketches is illustrated through a number of examples.

Learning General Policies for Classical Planning Domains: Getting Beyond C$_2$

GNN-based approaches for learning general policies across planning domains are limited by the expressive power of $C_2$, namely; first-order logic with two variables and counting. This limitation can be overcomed by transitioning to $k$-GNNs, for $k=3$, wherein object embeddings are substituted with triplet embeddings. Yet, while $3$-GNNs have the expressive power of $C_3$, unlike $1$- and $2$-GNNs that are confined to $C_2$, they require quartic time for message exchange and cubic space for embeddings, rendering them impractical. In this work, we introduce a parameterized version of relational GNNs. When $t$ is infinity, R-GNN[$t$] approximates $3$-GNNs using only quadratic space for embeddings. For lower values of $t$, such as $t=1$ and $t=2$, R-GNN[$t$] achieves a weaker approximation by exchanging fewer messages, yet interestingly, often yield the $C_3$ features required in several planning domains. Furthermore, the new R-GNN[$t$] architecture is the original R-GNN architecture with a suitable transformation applied to the input states only. Experimental results illustrate the clear performance gains of R-GNN[$1$] and R-GNN[$2$] over plain R-GNNs, and also over edge transformers that also approximate $3$-GNNs.

General Policies, Subgoal Structure, and Planning Width

It has been observed that many classical planning domains with atomic goals can be solved by means of a simple polynomial exploration procedure, called IW, that runs in time exponential in the problem width, which in these cases is bounded and small. Yet, while the notion of width has become part of state-of-the-art planning algorithms such as BFWS, there is no good explanation for why so many benchmark domains have bounded width when atomic goals are considered. In this work, we address this question by relating bounded width with the existence of general optimal policies that in each planning instance are represented by tuples of atoms of bounded size. We also define the notions of (explicit) serializations and serialized width that have a broader scope as many domains have a bounded serialized width but no bounded width. Such problems are solved non-optimally in polynomial time by a suitable variant of the Serialized IW algorithm. Finally, the language of general policies and the semantics of serializations are combined to yield a simple, meaningful, and expressive language for specifying serializations in compact form in the form of sketches, which can be used for encoding domain control knowledge by hand or for learning it from small examples. Sketches express general problem decompositions in terms of subgoals, and sketches of bounded width express problem decompositions that can be solved in polynomial time.