Symmetries and Expressive Requirements for Learning General Policies

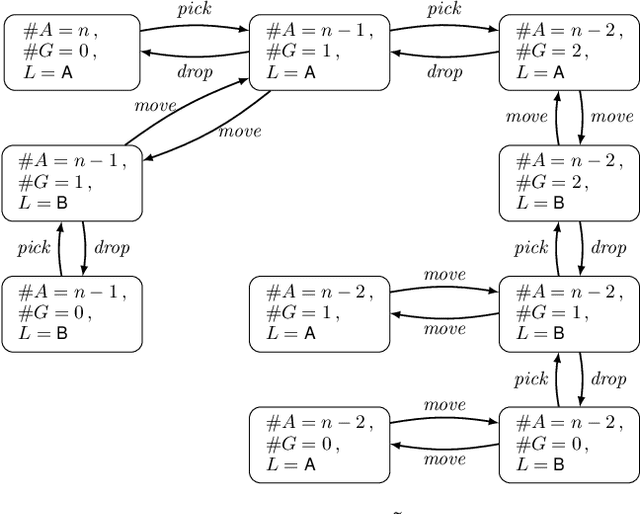
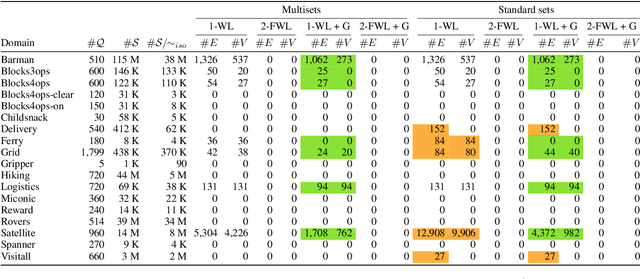
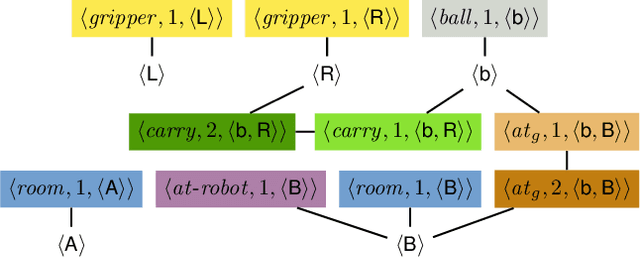
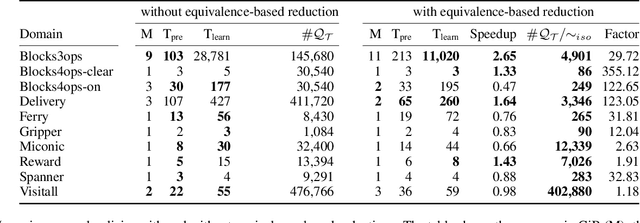
State symmetries play an important role in planning and generalized planning. In the first case, state symmetries can be used to reduce the size of the search; in the second, to reduce the size of the training set. In the case of general planning, however, it is also critical to distinguish non-symmetric states, i.e., states that represent non-isomorphic relational structures. However, while the language of first-order logic distinguishes non-symmetric states, the languages and architectures used to represent and learn general policies do not. In particular, recent approaches for learning general policies use state features derived from description logics or learned via graph neural networks (GNNs) that are known to be limited by the expressive power of C_2, first-order logic with two variables and counting. In this work, we address the problem of detecting symmetries in planning and generalized planning and use the results to assess the expressive requirements for learning general policies over various planning domains. For this, we map planning states to plain graphs, run off-the-shelf algorithms to determine whether two states are isomorphic with respect to the goal, and run coloring algorithms to determine if C_2 features computed logically or via GNNs distinguish non-isomorphic states. Symmetry detection results in more effective learning, while the failure to detect non-symmetries prevents general policies from being learned at all in certain domains.

On Policy Reuse: An Expressive Language for Representing and Executing General Policies that Call Other Policies

Recently, a simple but powerful language for expressing and learning general policies and problem decompositions (sketches) has been introduced in terms of rules defined over a set of Boolean and numerical features. In this work, we consider three extensions of this language aimed at making policies and sketches more flexible and reusable: internal memory states, as in finite state controllers; indexical features, whose values are a function of the state and a number of internal registers that can be loaded with objects; and modules that wrap up policies and sketches and allow them to call each other by passing parameters. In addition, unlike general policies that select state transitions rather than ground actions, the new language allows for the selection of such actions. The expressive power of the resulting language for policies and sketches is illustrated through a number of examples.

Learning General Policies for Classical Planning Domains: Getting Beyond C$_2$

GNN-based approaches for learning general policies across planning domains are limited by the expressive power of $C_2$, namely; first-order logic with two variables and counting. This limitation can be overcomed by transitioning to $k$-GNNs, for $k=3$, wherein object embeddings are substituted with triplet embeddings. Yet, while $3$-GNNs have the expressive power of $C_3$, unlike $1$- and $2$-GNNs that are confined to $C_2$, they require quartic time for message exchange and cubic space for embeddings, rendering them impractical. In this work, we introduce a parameterized version of relational GNNs. When $t$ is infinity, R-GNN[$t$] approximates $3$-GNNs using only quadratic space for embeddings. For lower values of $t$, such as $t=1$ and $t=2$, R-GNN[$t$] achieves a weaker approximation by exchanging fewer messages, yet interestingly, often yield the $C_3$ features required in several planning domains. Furthermore, the new R-GNN[$t$] architecture is the original R-GNN architecture with a suitable transformation applied to the input states only. Experimental results illustrate the clear performance gains of R-GNN[$1$] and R-GNN[$2$] over plain R-GNNs, and also over edge transformers that also approximate $3$-GNNs.

General Policies, Subgoal Structure, and Planning Width

It has been observed that many classical planning domains with atomic goals can be solved by means of a simple polynomial exploration procedure, called IW, that runs in time exponential in the problem width, which in these cases is bounded and small. Yet, while the notion of width has become part of state-of-the-art planning algorithms such as BFWS, there is no good explanation for why so many benchmark domains have bounded width when atomic goals are considered. In this work, we address this question by relating bounded width with the existence of general optimal policies that in each planning instance are represented by tuples of atoms of bounded size. We also define the notions of (explicit) serializations and serialized width that have a broader scope as many domains have a bounded serialized width but no bounded width. Such problems are solved non-optimally in polynomial time by a suitable variant of the Serialized IW algorithm. Finally, the language of general policies and the semantics of serializations are combined to yield a simple, meaningful, and expressive language for specifying serializations in compact form in the form of sketches, which can be used for encoding domain control knowledge by hand or for learning it from small examples. Sketches express general problem decompositions in terms of subgoals, and sketches of bounded width express problem decompositions that can be solved in polynomial time.

Language-Based Causal Representation Learning

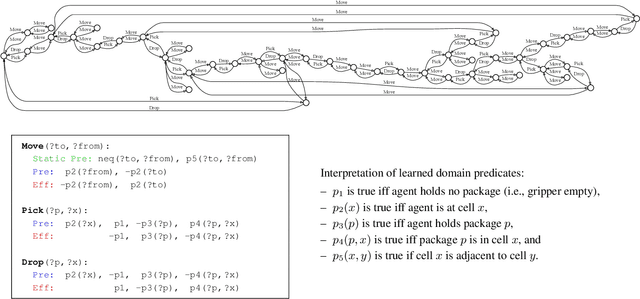
Consider the finite state graph that results from a simple, discrete, dynamical system in which an agent moves in a rectangular grid picking up and dropping packages. Can the state variables of the problem, namely, the agent location and the package locations, be recovered from the structure of the state graph alone without having access to information about the objects, the structure of the states, or any background knowledge? We show that this is possible provided that the dynamics is learned over a suitable domain-independent first-order causal language that makes room for objects and relations that are not assumed to be known. The preference for the most compact representation in the language that is compatible with the data provides a strong and meaningful learning bias that makes this possible. The language of structured causal models (SCMs) is the standard language for representing (static) causal models but in dynamic worlds populated by objects, first-order causal languages such as those used in "classical AI planning" are required. While "classical AI" requires handcrafted representations, similar representations can be learned from unstructured data over the same languages. Indeed, it is the languages and the preference for compact representations in those languages that provide structure to the world, uncovering objects, relations, and causes.

Learning Generalized Policies Without Supervision Using GNNs

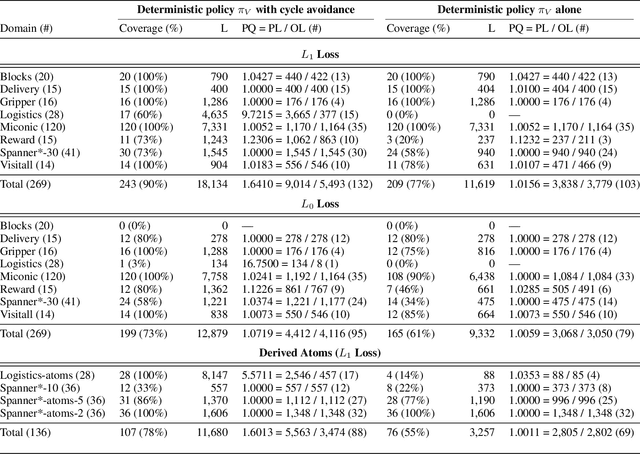
We consider the problem of learning generalized policies for classical planning domains using graph neural networks from small instances represented in lifted STRIPS. The problem has been considered before but the proposed neural architectures are complex and the results are often mixed. In this work, we use a simple and general GNN architecture and aim at obtaining crisp experimental results and a deeper understanding: either the policy greedy in the learned value function achieves close to 100% generalization over instances larger than those used in training, or the failure must be understood, and possibly fixed, logically. For this, we exploit the relation established between the expressive power of GNNs and the $C_{2}$ fragment of first-order logic (namely, FOL with 2 variables and counting quantifiers). We find for example that domains with general policies that require more expressive features can be solved with GNNs once the states are extended with suitable "derived atoms" encoding role compositions and transitive closures that do not fit into $C_{2}$. The work follows the GNN approach for learning optimal general policies in a supervised fashion (Stahlberg, Bonet, Geffner, 2022); but the learned policies are no longer required to be optimal (which expands the scope, as many planning domains do not have general optimal policies) and are learned without supervision. Interestingly, value-based reinforcement learning methods that aim to produce optimal policies, do not always yield policies that generalize, as the goals of optimality and generality are in conflict in domains where optimal planning is NP-hard.

Learning First-Order Symbolic Planning Representations That Are Grounded

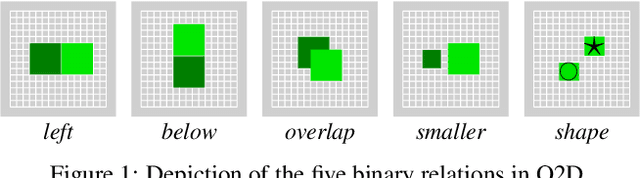
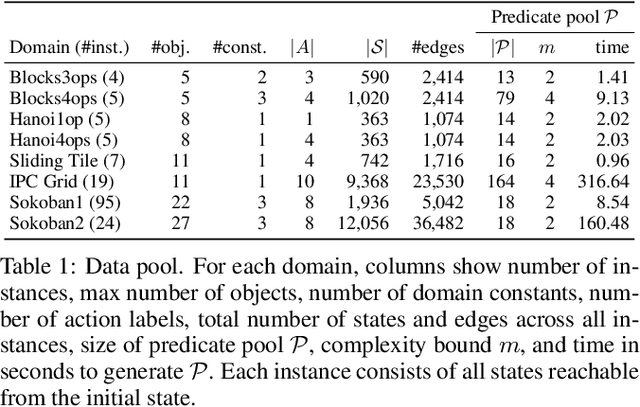
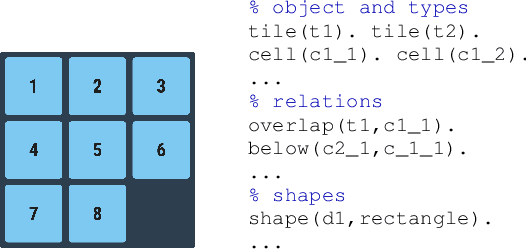
Two main approaches have been developed for learning first-order planning (action) models from unstructured data: combinatorial approaches that yield crisp action schemas from the structure of the state space, and deep learning approaches that produce action schemas from states represented by images. A benefit of the former approach is that the learned action schemas are similar to those that can be written by hand; a benefit of the latter is that the learned representations (predicates) are grounded on the images, and as a result, new instances can be given in terms of images. In this work, we develop a new formulation for learning crisp first-order planning models that are grounded on parsed images, a step to combine the benefits of the two approaches. Parsed images are assumed to be given in a simple O2D language (objects in 2D) that involves a small number of unary and binary predicates like "left", "above", "shape", etc. After learning, new planning instances can be given in terms of pairs of parsed images, one for the initial situation and the other for the goal. Learning and planning experiments are reported for several domains including Blocks, Sokoban, IPC Grid, and Hanoi.

Learning General Optimal Policies with Graph Neural Networks: Expressive Power, Transparency, and Limits

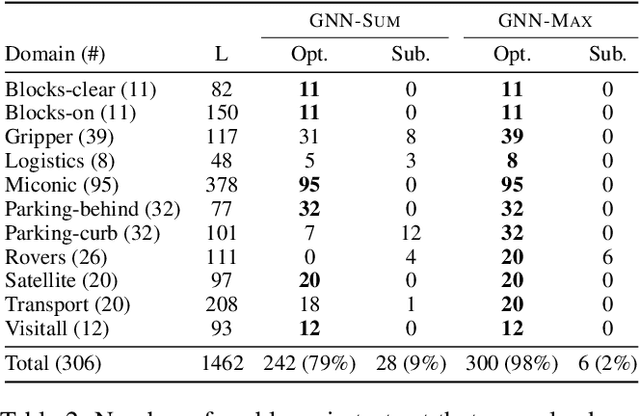
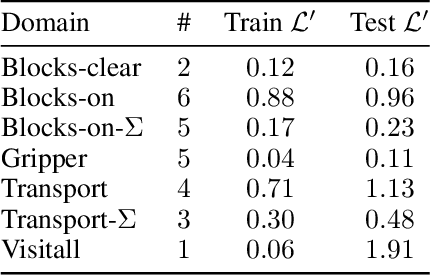
It has been recently shown that general policies for many classical planning domains can be expressed and learned in terms of a pool of features defined from the domain predicates using a description logic grammar. At the same time, most description logics correspond to a fragment of $k$-variable counting logic ($C_k$) for $k=2$, that has been shown to provide a tight characterization of the expressive power of graph neural networks. In this work, we make use of these results to understand the power and limits of using graph neural networks (GNNs) for learning optimal general policies over a number of tractable planning domains where such policies are known to exist. For this, we train a simple GNN in a supervised manner to approximate the optimal value function $V^{*}(s)$ of a number of sample states $s$. As predicted by the theory, it is observed that general optimal policies are obtained in domains where general optimal value functions can be defined with $C_2$ features but not in those requiring more expressive $C_3$ features. In addition, it is observed that the features learned are in close correspondence with the features needed to express $V^{*}$ in closed form. The theory and the analysis of the domains let us understand the features that are actually learned as well as those that cannot be learned in this way, and let us move in a principled manner from a combinatorial optimization approach to learning general policies to a potentially, more robust and scalable approach based on deep learning.

Learning First-Order Representations for Planning from Black-Box States: New Results

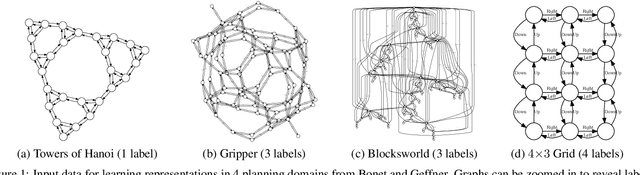
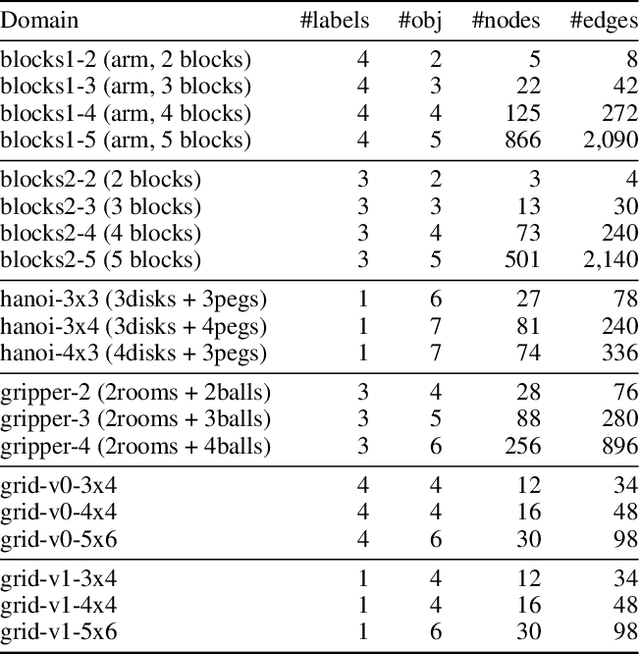
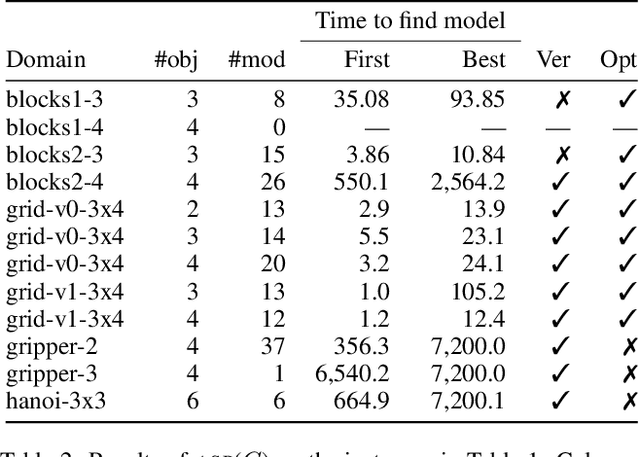
Recently Bonet and Geffner have shown that first-order representations for planning domains can be learned from the structure of the state space without any prior knowledge about the action schemas or domain predicates. For this, the learning problem is formulated as the search for a simplest first-order domain description D that along with information about instances I_i (number of objects and initial state) determine state space graphs G(P_i) that match the observed state graphs G_i where P_i = (D, I_i). The search is cast and solved approximately by means of a SAT solver that is called over a large family of propositional theories that differ just in the parameters encoding the possible number of action schemas and domain predicates, their arities, and the number of objects. In this work, we push the limits of these learners by moving to an answer set programming (ASP) encoding using the CLINGO system. The new encodings are more transparent and concise, extending the range of possible models while facilitating their exploration. We show that the domains introduced by Bonet and Geffner can be solved more efficiently in the new approach, often optimally, and furthermore, that the approach can be easily extended to handle partial information about the state graphs as well as noise that prevents some states from being distinguished.

Flexible FOND Planning with Explicit Fairness Assumptions

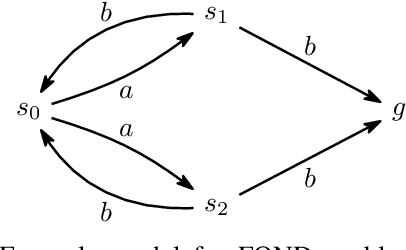
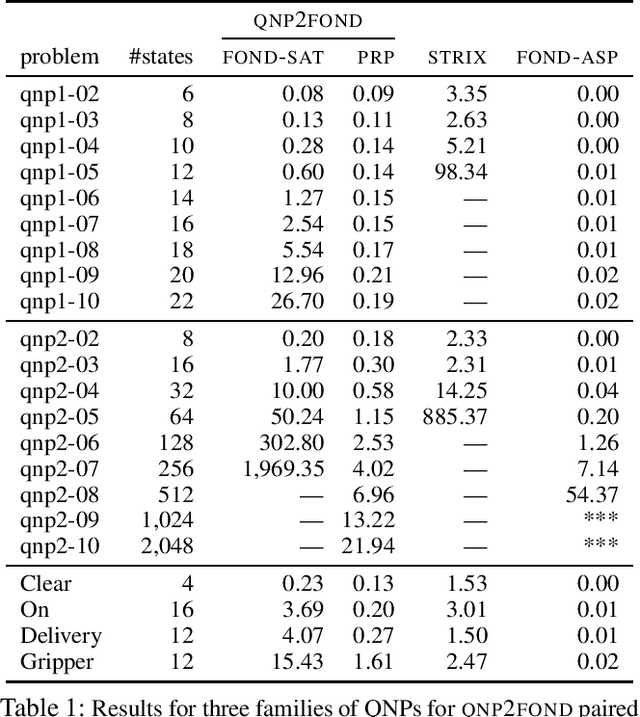
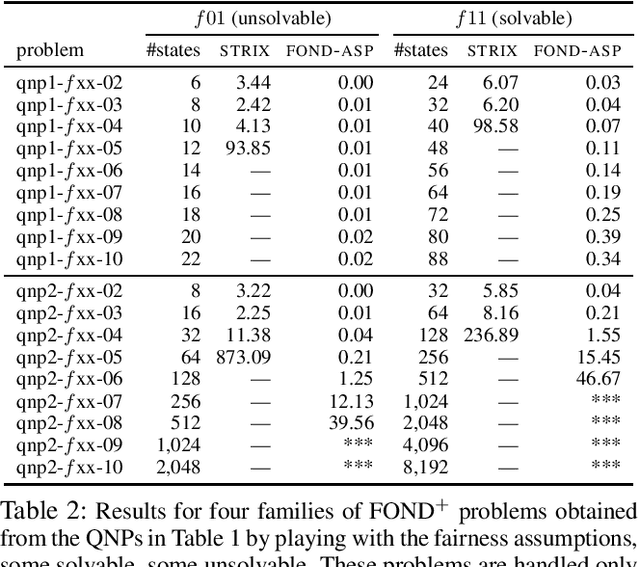
We consider the problem of reaching a propositional goal condition in fully-observable non-deterministic (FOND) planning under a general class of fairness assumptions that are given explicitly. The fairness assumptions are of the form A/B and say that state trajectories that contain infinite occurrences of an action a from A in a state s and finite occurrence of actions from B, must also contain infinite occurrences of action a in s followed by each one of its possible outcomes. The infinite trajectories that violate this condition are deemed as unfair, and the solutions are policies for which all the fair trajectories reach a goal state. We show that strong and strong-cyclic FOND planning, as well as QNP planning, a planning model introduced recently for generalized planning, are all special cases of FOND planning with fairness assumptions of this form which can also be combined. FOND+ planning, as this form of planning is called, combines the syntax of FOND planning with some of the versatility of LTL for expressing fairness constraints. A new planner is implemented by reducing FOND+ planning to answer set programs, and the performance of the planner is evaluated in comparison with FOND and QNP planners, and LTL synthesis tools.