Learning Generalized Policies Without Supervision Using GNNs
Paper and Code
May 12, 2022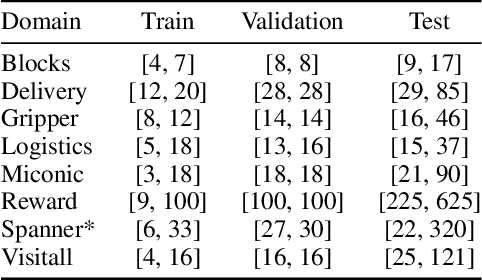
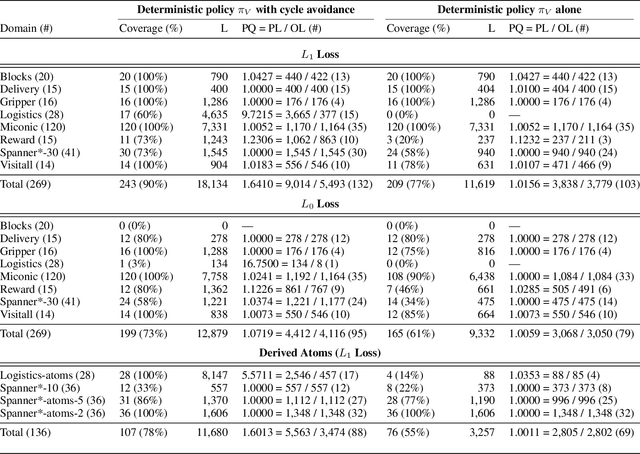
We consider the problem of learning generalized policies for classical planning domains using graph neural networks from small instances represented in lifted STRIPS. The problem has been considered before but the proposed neural architectures are complex and the results are often mixed. In this work, we use a simple and general GNN architecture and aim at obtaining crisp experimental results and a deeper understanding: either the policy greedy in the learned value function achieves close to 100% generalization over instances larger than those used in training, or the failure must be understood, and possibly fixed, logically. For this, we exploit the relation established between the expressive power of GNNs and the $C_{2}$ fragment of first-order logic (namely, FOL with 2 variables and counting quantifiers). We find for example that domains with general policies that require more expressive features can be solved with GNNs once the states are extended with suitable "derived atoms" encoding role compositions and transitive closures that do not fit into $C_{2}$. The work follows the GNN approach for learning optimal general policies in a supervised fashion (Stahlberg, Bonet, Geffner, 2022); but the learned policies are no longer required to be optimal (which expands the scope, as many planning domains do not have general optimal policies) and are learned without supervision. Interestingly, value-based reinforcement learning methods that aim to produce optimal policies, do not always yield policies that generalize, as the goals of optimality and generality are in conflict in domains where optimal planning is NP-hard.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge