Learning First-Order Symbolic Planning Representations That Are Grounded

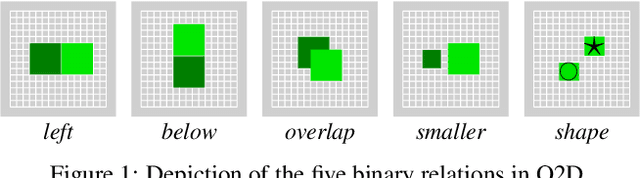
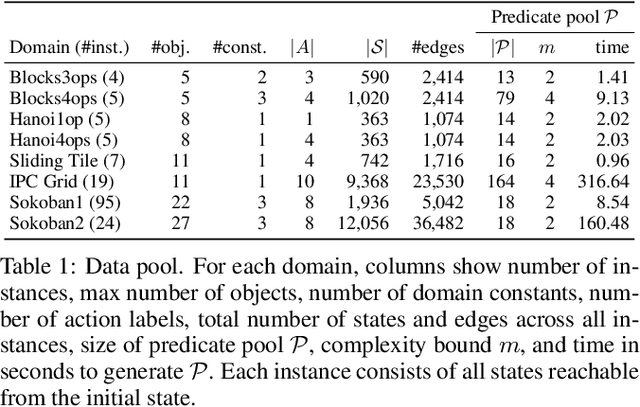
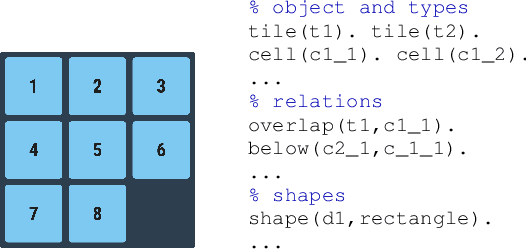
Two main approaches have been developed for learning first-order planning (action) models from unstructured data: combinatorial approaches that yield crisp action schemas from the structure of the state space, and deep learning approaches that produce action schemas from states represented by images. A benefit of the former approach is that the learned action schemas are similar to those that can be written by hand; a benefit of the latter is that the learned representations (predicates) are grounded on the images, and as a result, new instances can be given in terms of images. In this work, we develop a new formulation for learning crisp first-order planning models that are grounded on parsed images, a step to combine the benefits of the two approaches. Parsed images are assumed to be given in a simple O2D language (objects in 2D) that involves a small number of unary and binary predicates like "left", "above", "shape", etc. After learning, new planning instances can be given in terms of pairs of parsed images, one for the initial situation and the other for the goal. Learning and planning experiments are reported for several domains including Blocks, Sokoban, IPC Grid, and Hanoi.

Learning to Act and Observe in Partially Observable Domains

We consider a learning agent in a partially observable environment, with which the agent has never interacted before, and about which it learns both what it can observe and how its actions affect the environment. The agent can learn about this domain from experience gathered by taking actions in the domain and observing their results. We present learning algorithms capable of learning as much as possible (in a well-defined sense) both about what is directly observable and about what actions do in the domain, given the learner's observational constraints. We differentiate the level of domain knowledge attained by each algorithm, and characterize the type of observations required to reach it. The algorithms use dynamic epistemic logic (DEL) to represent the learned domain information symbolically. Our work continues that of Bolander and Gierasimczuk (2015), which developed DEL-based learning algorithms based to learn domain information in fully observable domains.

Dynamic Term-Modal Logics for Epistemic Planning

Classical planning frameworks are built on first-order languages. The first-order expressive power is desirable for compactly representing actions via schemas, and for specifying goal formulas such as $\neg\exists x\mathsf{blocks\_door}(x)$. In contrast, several recent epistemic planning frameworks build on propositional modal logic. The modal expressive power is desirable for investigating planning problems with epistemic goals such as $K_{a}\neg\mathsf{problem}$. The present paper presents an epistemic planning framework with first-order expressiveness of classical planning, but extending fully to the epistemic operators. In this framework, e.g. $\exists xK_{x}\exists y\mathsf{blocks\_door}(y)$ is a formula. Logics with this expressive power are called "term-modal" in the literature. This paper presents a rich but well-behaved semantics for term-modal logic. The semantics are given a dynamic extension using first-order "action models" allowing for epistemic planning, and it is shown how corresponding "action schemas" allow for a very compact action representation. Concerning metatheory, the paper defines axiomatic normal term-modal logics, shows a Canonical Model Theorem-like result, present non-standard frame characterization formulas, shows decidability for the finite agent case, and shows a general completeness result for the dynamic extension by reduction axioms.