Language-Based Causal Representation Learning
Paper and Code
Jul 12, 2022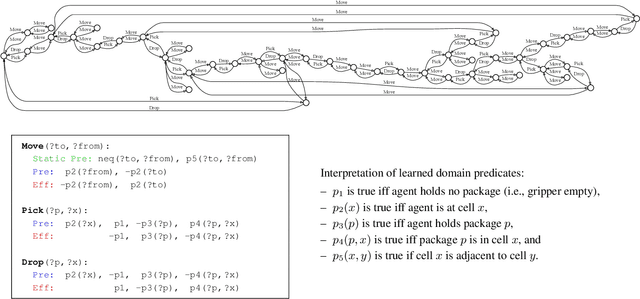
Consider the finite state graph that results from a simple, discrete, dynamical system in which an agent moves in a rectangular grid picking up and dropping packages. Can the state variables of the problem, namely, the agent location and the package locations, be recovered from the structure of the state graph alone without having access to information about the objects, the structure of the states, or any background knowledge? We show that this is possible provided that the dynamics is learned over a suitable domain-independent first-order causal language that makes room for objects and relations that are not assumed to be known. The preference for the most compact representation in the language that is compatible with the data provides a strong and meaningful learning bias that makes this possible. The language of structured causal models (SCMs) is the standard language for representing (static) causal models but in dynamic worlds populated by objects, first-order causal languages such as those used in "classical AI planning" are required. While "classical AI" requires handcrafted representations, similar representations can be learned from unstructured data over the same languages. Indeed, it is the languages and the preference for compact representations in those languages that provide structure to the world, uncovering objects, relations, and causes.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge