Learning Sketches for Decomposing Planning Problems into Subproblems of Bounded Width: Extended Version
Paper and Code
Mar 28, 2022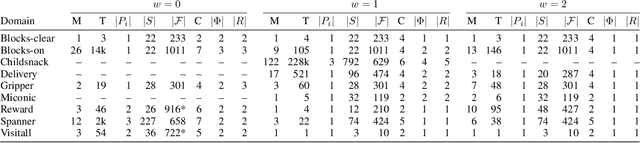
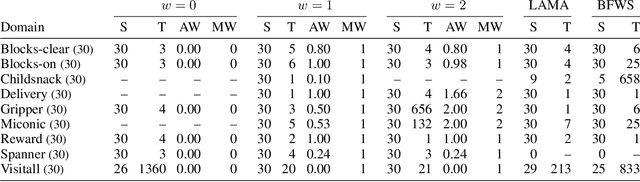
Recently, sketches have been introduced as a general language for representing the subgoal structure of instances drawn from the same domain. Sketches are collections of rules of the form C -> E over a given set of features where C expresses Boolean conditions and E expresses qualitative changes. Each sketch rule defines a subproblem: going from a state that satisfies C to a state that achieves the change expressed by E or a goal state. Sketches can encode simple goal serializations, general policies, or decompositions of bounded width that can be solved greedily, in polynomial time, by the SIW_R variant of the SIW algorithm. Previous work has shown the computational value of sketches over benchmark domains that, while tractable, are challenging for domain-independent planners. In this work, we address the problem of learning sketches automatically given a planning domain, some instances of the target class of problems, and the desired bound on the sketch width. We present a logical formulation of the problem, an implementation using the ASP solver Clingo, and experimental results. The sketch learner and the SIW_R planner yield a domain-independent planner that learns and exploits domain structure in a crisp and explicit form.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge