Classical Planning with LLM-Generated Heuristics: Challenging the State of the Art with Python Code

In recent years, large language models (LLMs) have shown remarkable capabilities in various artificial intelligence problems. However, they fail to plan reliably, even when prompted with a detailed definition of the planning task. Attempts to improve their planning capabilities, such as chain-of-thought prompting, fine-tuning, and explicit "reasoning" still yield incorrect plans and usually fail to generalize to larger tasks. In this paper, we show how to use LLMs to generate correct plans, even for out-of-distribution tasks of increasing size. For a given planning domain, we ask an LLM to generate several domain-dependent heuristic functions in the form of Python code, evaluate them on a set of training tasks within a greedy best-first search, and choose the strongest one. The resulting LLM-generated heuristics solve many more unseen test tasks than state-of-the-art domain-independent heuristics for classical planning. They are even competitive with the strongest learning algorithm for domain-dependent planning. These findings are especially remarkable given that our proof-of-concept implementation is based on an unoptimized Python planner and the baselines all build upon highly optimized C++ code. In some domains, the LLM-generated heuristics expand fewer states than the baselines, revealing that they are not only efficiently computable, but sometimes even more informative than the state-of-the-art heuristics. Overall, our results show that sampling a set of planning heuristic function programs can significantly improve the planning capabilities of LLMs.

Goal Recognition via Linear Programming

Goal Recognition is the task by which an observer aims to discern the goals that correspond to plans that comply with the perceived behavior of subject agents given as a sequence of observations. Research on Goal Recognition as Planning encompasses reasoning about the model of a planning task, the observations, and the goals using planning techniques, resulting in very efficient recognition approaches. In this article, we design novel recognition approaches that rely on the Operator-Counting framework, proposing new constraints, and analyze their constraints' properties both theoretically and empirically. The Operator-Counting framework is a technique that efficiently computes heuristic estimates of cost-to-goal using Integer/Linear Programming (IP/LP). In the realm of theory, we prove that the new constraints provide lower bounds on the cost of plans that comply with observations. We also provide an extensive empirical evaluation to assess how the new constraints improve the quality of the solution, and we found that they are especially informed in deciding which goals are unlikely to be part of the solution. Our novel recognition approaches have two pivotal advantages: first, they employ new IP/LP constraints for efficiently recognizing goals; second, we show how the new IP/LP constraints can improve the recognition of goals under both partial and noisy observability.

Iterative Depth-First Search for Fully Observable Non-Deterministic Planning

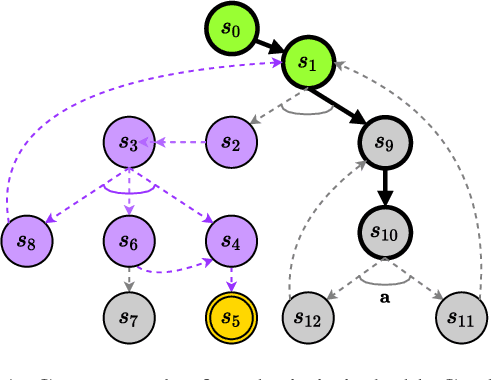
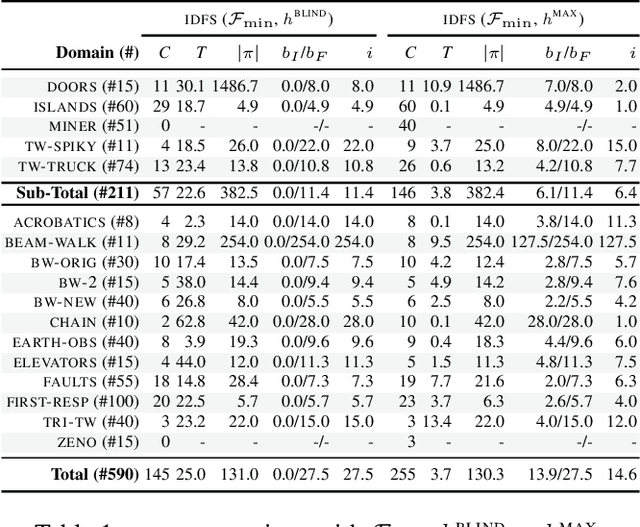
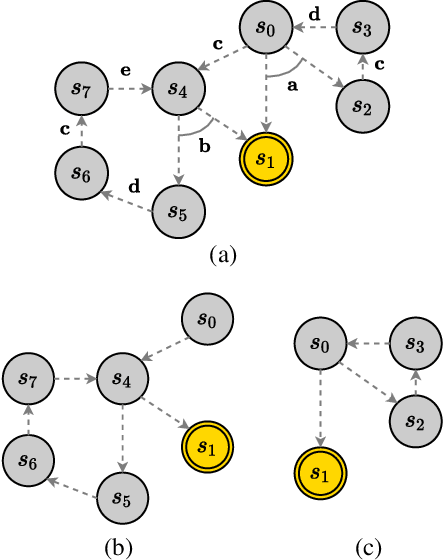
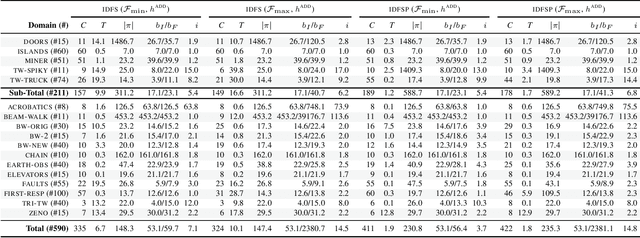
Fully Observable Non-Deterministic (FOND) planning models uncertainty through actions with non-deterministic effects. Existing FOND planning algorithms are effective and employ a wide range of techniques. However, most of the existing algorithms are not robust for dealing with both non-determinism and task size. In this paper, we develop a novel iterative depth-first search algorithm that solves FOND planning tasks and produces strong cyclic policies. Our algorithm is explicitly designed for FOND planning, addressing more directly the non-deterministic aspect of FOND planning, and it also exploits the benefits of heuristic functions to make the algorithm more effective during the iterative searching process. We compare our proposed algorithm to well-known FOND planners, and show that it has robust performance over several distinct types of FOND domains considering different metrics.

Procedural Generation of Initial States of Sokoban

Procedural generation of initial states of state-space search problems have applications in human and machine learning as well as in the evaluation of planning systems. In this paper we deal with the task of generating hard and solvable initial states of Sokoban puzzles. We propose hardness metrics based on pattern database heuristics and the use of novelty to improve the exploration of search methods in the task of generating initial states. We then present a system called Beta that uses our hardness metrics and novelty to generate initial states. Experiments show that Beta is able to generate initial states that are harder to solve by a specialized solver than those designed by human experts.