3D Point Cloud Denoising via Deep Neural Network based Local Surface Estimation

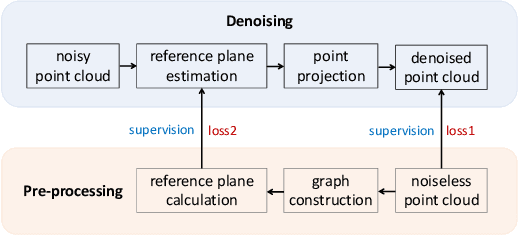
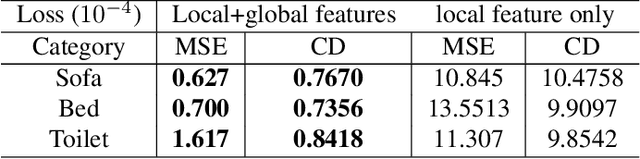
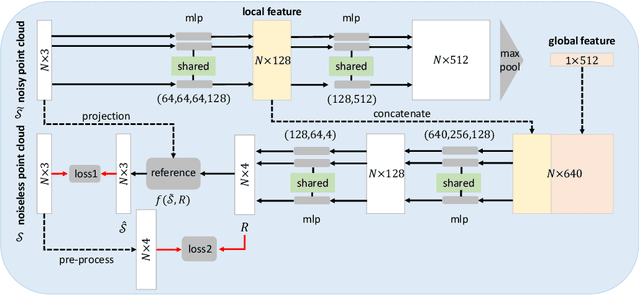
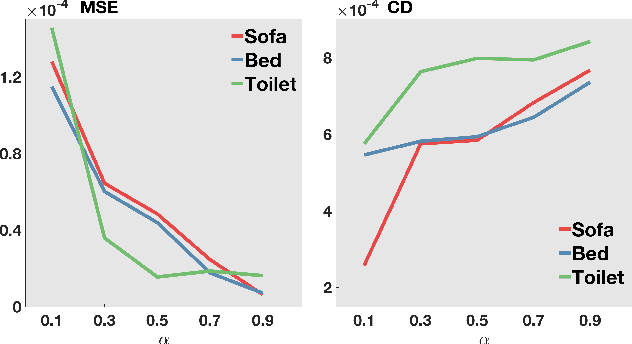
We present a neural-network-based architecture for 3D point cloud denoising called neural projection denoising (NPD). In our previous work, we proposed a two-stage denoising algorithm, which first estimates reference planes and follows by projecting noisy points to estimated reference planes. Since the estimated reference planes are inevitably noisy, multi-projection is applied to stabilize the denoising performance. NPD algorithm uses a neural network to estimate reference planes for points in noisy point clouds. With more accurate estimations of reference planes, we are able to achieve better denoising performances with only one-time projection. To the best of our knowledge, NPD is the first work to denoise 3D point clouds with deep learning techniques. To conduct the experiments, we sample 40000 point clouds from the 3D data in ShapeNet to train a network and sample 350 point clouds from the 3D data in ModelNet10 to test. Experimental results show that our algorithm can estimate normal vectors of points in noisy point clouds. Comparing to five competitive methods, the proposed algorithm achieves better denoising performance and produces much smaller variances.

Rotation Invariant Angular Descriptor Via A Bandlimited Gaussian-like Kernel

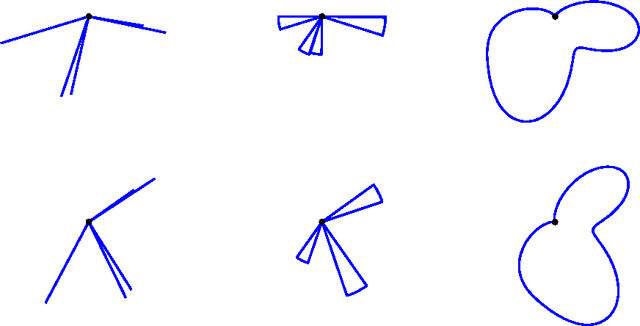
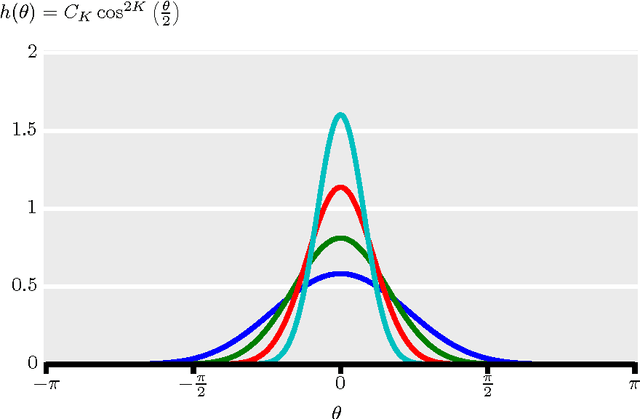
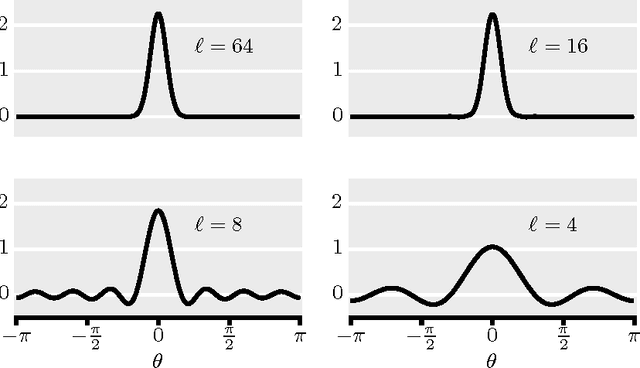
We present a new smooth, Gaussian-like kernel that allows the kernel density estimate for an angular distribution to be exactly represented by a finite number of its Fourier series coefficients. Distributions of angular quantities, such as gradients, are a central part of several state-of-the-art image processing algorithms, but these distributions are usually described via histograms and therefore lack rotation invariance due to binning artifacts. Replacing histograming with kernel density estimation removes these binning artifacts and can provide a finite-dimensional descriptor of the distribution, provided that the kernel is selected to be bandlimited. In this paper, we present a new band-limited kernel that has the added advantage of being Gaussian-like in the angular domain. We then show that it compares favorably to gradient histograms for patch matching, person detection, and texture segmentation.

Performance measures for classification systems with rejection

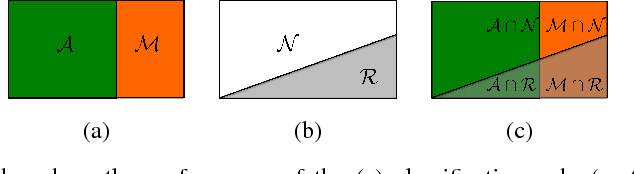
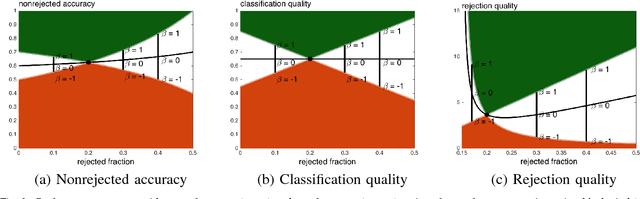
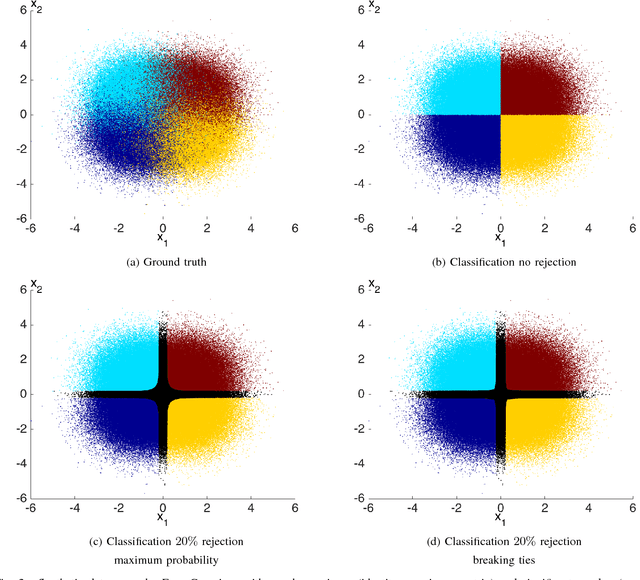
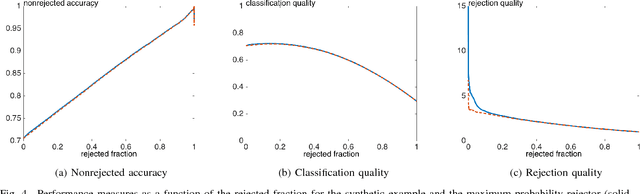
Classifiers with rejection are essential in real-world applications where misclassifications and their effects are critical. However, if no problem specific cost function is defined, there are no established measures to assess the performance of such classifiers. We introduce a set of desired properties for performance measures for classifiers with rejection, based on which we propose a set of three performance measures for the evaluation of the performance of classifiers with rejection that satisfy the desired properties. The nonrejected accuracy measures the ability of the classifier to accurately classify nonrejected samples; the classification quality measures the correct decision making of the classifier with rejector; and the rejection quality measures the ability to concentrate all misclassified samples onto the set of rejected samples. From the measures, we derive the concept of relative optimality that allows us to connect the measures to a family of cost functions that take into account the trade-off between rejection and misclassification. We illustrate the use of the proposed performance measures on classifiers with rejection applied to synthetic and real-world data.

Robust hyperspectral image classification with rejection fields

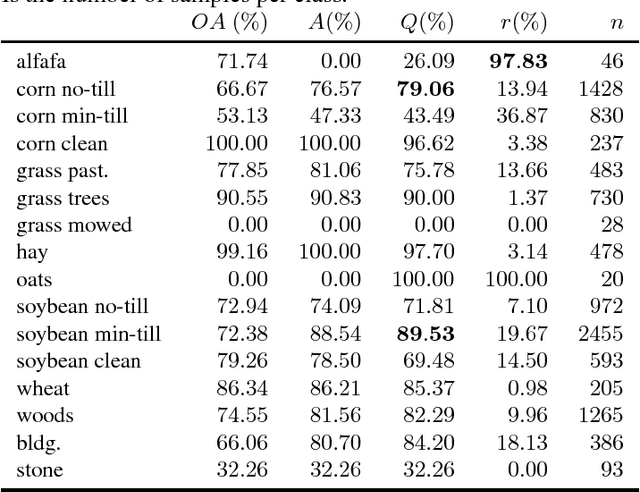
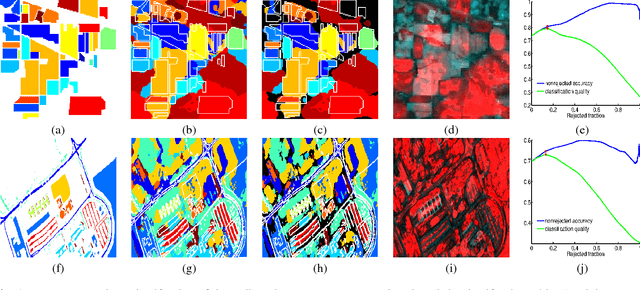
In this paper we present a novel method for robust hyperspectral image classification using context and rejection. Hyperspectral image classification is generally an ill-posed image problem where pixels may belong to unknown classes, and obtaining representative and complete training sets is costly. Furthermore, the need for high classification accuracies is frequently greater than the need to classify the entire image. We approach this problem with a robust classification method that combines classification with context with classification with rejection. A rejection field that will guide the rejection is derived from the classification with contextual information obtained by using the SegSALSA algorithm. We validate our method in real hyperspectral data and show that the performance gains obtained from the rejection fields are equivalent to an increase the dimension of the training sets.

SegSALSA-STR: A convex formulation to supervised hyperspectral image segmentation using hidden fields and structure tensor regularization

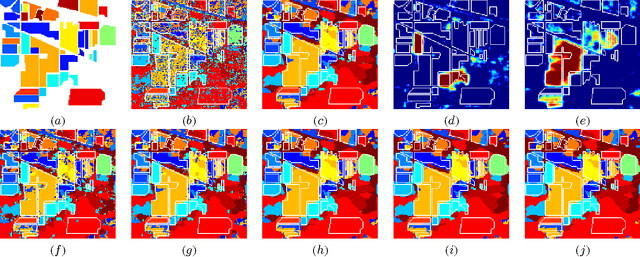
We present a supervised hyperspectral image segmentation algorithm based on a convex formulation of a marginal maximum a posteriori segmentation with hidden fields and structure tensor regularization: Segmentation via the Constraint Split Augmented Lagrangian Shrinkage by Structure Tensor Regularization (SegSALSA-STR). This formulation avoids the generally discrete nature of segmentation problems and the inherent NP-hardness of the integer optimization associated. We extend the Segmentation via the Constraint Split Augmented Lagrangian Shrinkage (SegSALSA) algorithm by generalizing the vectorial total variation prior using a structure tensor prior constructed from a patch-based Jacobian. The resulting algorithm is convex, time-efficient and highly parallelizable. This shows the potential of combining hidden fields with convex optimization through the inclusion of different regularizers. The SegSALSA-STR algorithm is validated in the segmentation of real hyperspectral images.

Guaranteeing Convergence of Iterative Skewed Voting Algorithms for Image Segmentation

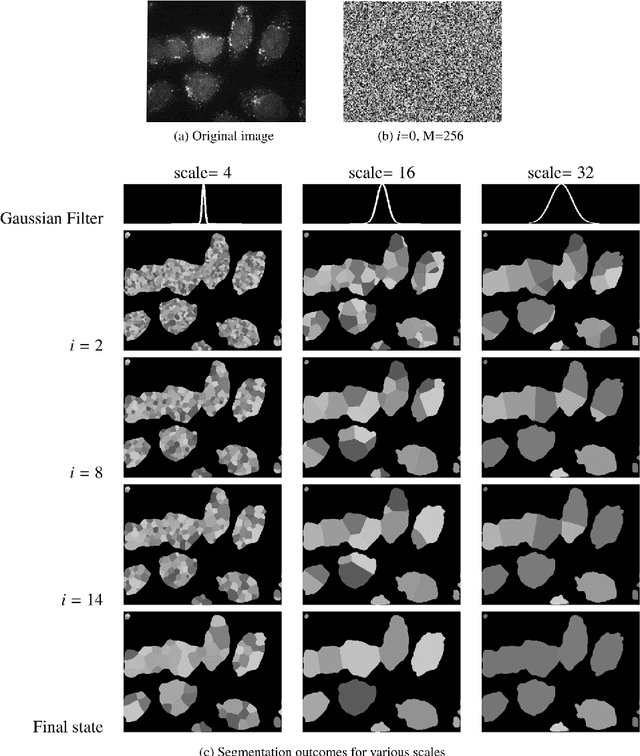
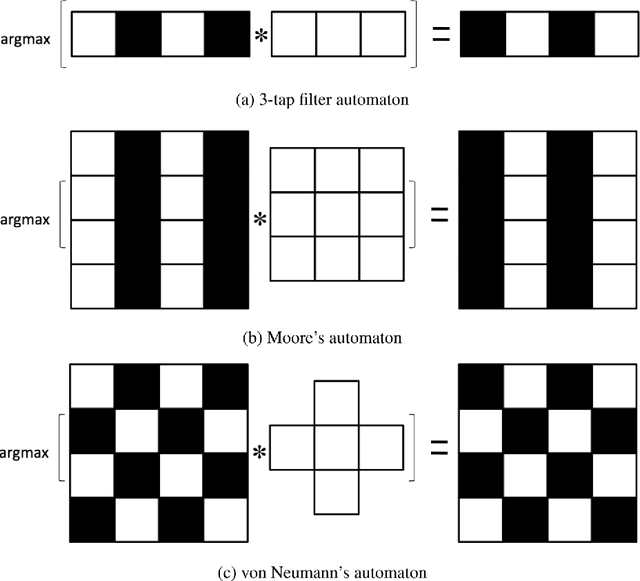
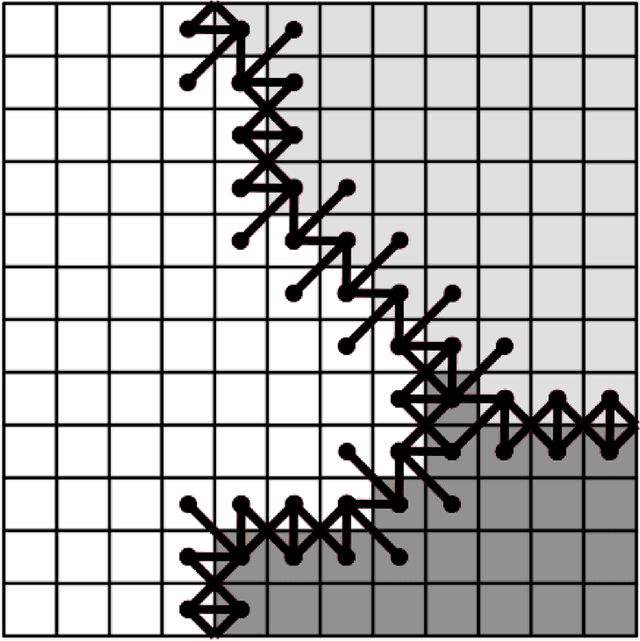
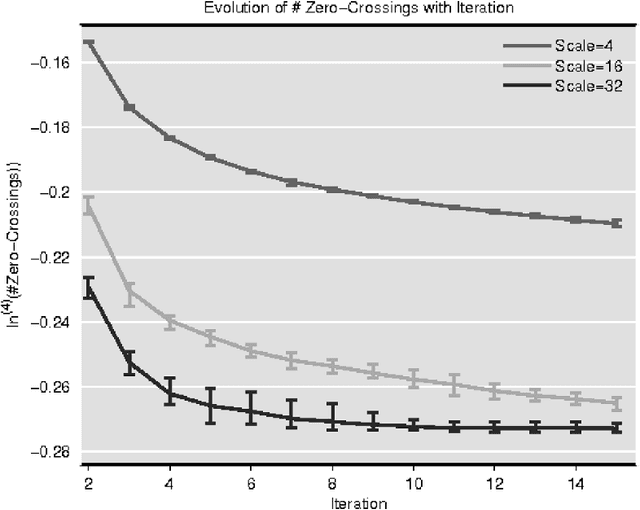
In this paper we provide rigorous proof for the convergence of an iterative voting-based image segmentation algorithm called Active Masks. Active Masks (AM) was proposed to solve the challenging task of delineating punctate patterns of cells from fluorescence microscope images. Each iteration of AM consists of a linear convolution composed with a nonlinear thresholding; what makes this process special in our case is the presence of additive terms whose role is to "skew" the voting when prior information is available. In real-world implementation, the AM algorithm always converges to a fixed point. We study the behavior of AM rigorously and present a proof of this convergence. The key idea is to formulate AM as a generalized (parallel) majority cellular automaton, adapting proof techniques from discrete dynamical systems.