Rotation Invariant Angular Descriptor Via A Bandlimited Gaussian-like Kernel
Paper and Code
Jun 08, 2016
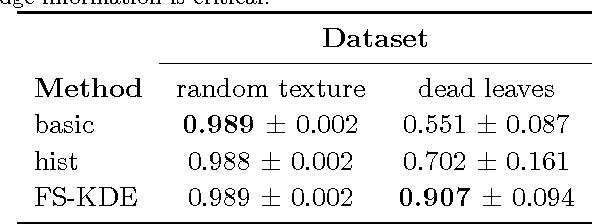
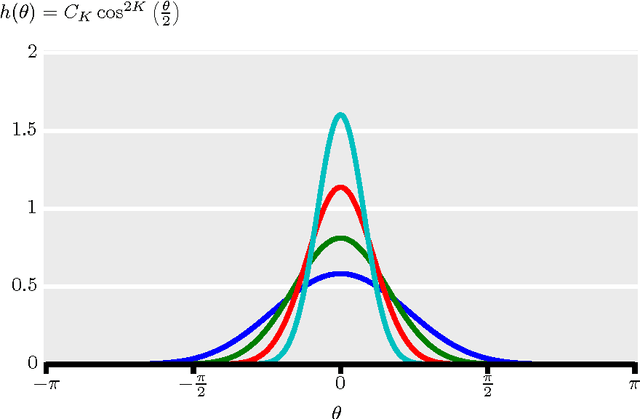
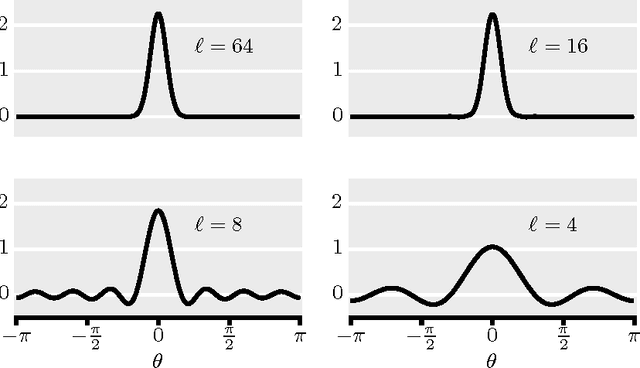
We present a new smooth, Gaussian-like kernel that allows the kernel density estimate for an angular distribution to be exactly represented by a finite number of its Fourier series coefficients. Distributions of angular quantities, such as gradients, are a central part of several state-of-the-art image processing algorithms, but these distributions are usually described via histograms and therefore lack rotation invariance due to binning artifacts. Replacing histograming with kernel density estimation removes these binning artifacts and can provide a finite-dimensional descriptor of the distribution, provided that the kernel is selected to be bandlimited. In this paper, we present a new band-limited kernel that has the added advantage of being Gaussian-like in the angular domain. We then show that it compares favorably to gradient histograms for patch matching, person detection, and texture segmentation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge